Supongamos que por los puntos A y B pasan planos perpendiculares a la dirección x, que determinan en el sólido las áreas S1 y S2 que poseen respectivamente, temperatura uniforme (superficies isotermas).
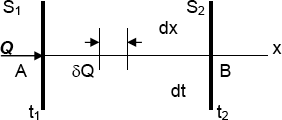
Si la temperatura es función lineal de x, la gradiente de temperatura tendrá el mismo valor entre los puntos A y B. Llamando δQ a la cantidad de calor transmitida en un tiempo dτ, en dirección x , por la superficie S, se cumple que:
δQ = λ . S . dτ . dt/dx
Si hacemos S = 1m2 ; dt = 1ºC ; dx = 1m; y dτ= 1 seg. , resulta δQ = λ = coeficiente de conductibilidad térmica.
Podemos definir entonces el coeficiente de conductibilidad térmica como la cantidad de calor que se transmite en un segundo, a través de la unidad de superficie, entre dos planos paralelos distantes la unidad de longitud y cuando la diferencia de sus temperaturas es de 1°C.
Unidades del coeficiente de conductibilidad
Si despejamos el valor de λ de la expresión de Fourier tenemos:
![]()
En el sistema internacional o SI, el que adopta en nuestro país para las normas IRAM, denominado SIMELA, el coeficiente de conductibilidad térmica será:
![]()
En otros sistemas las unidades de λ, son, por ejemplo en el sistema c.g.s.:
![]()
O en el sistema técnico:
![]()
Valores del coeficiente de conductibilidad
El valor numérico de λ depende del material del cuerpo.
Veamos algunos valores para buenos y malos conductores, a 0° C.
MATERIAL |
λ ( cal / m . °C. h) |
Característica |
|---|---|---|
Plata |
360 |
Muy Bueno |
Cobre |
335 |
Bueno |
Lana de vidrio |
0,032 |
Malo |
Corcho molido |
0,011 |
Muy Malo |
En los metales, pequeñas cantidades de impurezas pueden modificar considerablemente el valor de λ. Así por ejemplo, bastan trozos de arsénico en el cobre para reducir su conductividad térmica hasta cerca de la tercera parte de la correspondiente al cobre puro. Este proceso se denomina dopado, y se utiliza en la fabricación de semiconductores que se usan en la industria electrónica.
En la mayoría de los sólidos homogéneos, el valor de λ es función de la temperatura según una variación lineal:
λt = λ0 + a . t λ0 = coef. de conductibidad a 0°C.
Para materiales no homogéneos, el coeficiente λ a una temperatura dada es proporcional a la densidad aparente del material considerado.
Así por ejemplo, la lana de amianto posee los siguientes valores de λ a 0°C:
Densidad aparente (Kg /m lt) |
λ |
|---|---|
0,40 |
0,077 |
0,70 |
0,165 |
Flujo Calorífico
La ley de Fourier establece:
δQ = - λ . S . d τ . dt/dx
Se denomina flujo calorífico ϕ (fi) a la relación:
![]()
y expresa la cantidad de calor que se transmite en la unidad de tiempo. Entonces:
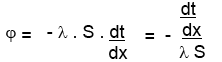
La expresión ![]() se denomina resistencia térmica
se denomina resistencia térmica
Por lo tanto:
![]()
En la expresión del flujo calorífico, se observa que depende de la diferencia de temperatura, en consecuencia, cuando la diferencia de temperaturas permanece constante, el flujo también será constante. Esto ocurre en el estado de régimen estacionario o permanente, pues la distribución de temperaturas es constante lo que mantiene constante la diferencia de temperaturas.
Por lo contrario, en el estado de régimen térmico variable, la distribución de las temperaturas varía con el tiempo, y también variará la diferencia de temperaturas, en consecuencia el flujo será variable.