Todos los cuerpos, cualquiera sea su temperatura, emiten energía en forma continua desde sus superficies. Esta energía se denomina energía radiante y es transportada por ondas electromagnéticas, por este motivo, la energía radiante puede transmitirse aún en el vacío. La emisión continua de energía radiante por un cuerpo se denomina radiación.
Como consecuencia de este fenómeno, dos cuerpos colocados en el vacío que están a diferentes temperaturas alcanzan el equilibrio térmico debido a que el de menor temperatura recibe energía radiante del otro cuerpo de mayor temperatura. Cuando la energía radiante es absorbida por un cuerpo, se transforma en calor; no obstante la energía radiante también puede ser reflejada (difundida) o refractada (propagada) por los cuerpos. Trataremos únicamente la energía radiante emitida por los sólidos y los líquidos, pues la emitida por los gases obedece a leyes muy diferentes.
Hemos dicho que la energía radiante se transmite por ondas electromagnéticas, por lo tanto su velocidad de propagación será la de la luz (300.000 km/seg en el vacío).
Las ondas electromagnéticas comprenden: radio ondas, ondas infrarrojas, luz visible, ondas ultravioletas y rayos X y γ; todas diferentes solamente en sus longitudes de ondas. Los cuerpos sólidos y líquidos emiten energía radiante que contiene ondas de todas las frecuencias, cuyas amplitudes dependen principalmente de la temperatura del cuerpo emisor y no del tipo de moléculas que lo formen.
En cambio, los gases, emiten energía radiante de relativamente pocas frecuencias, las cuales son características de las moléculas del gas.
Si la radiación emitida por un cuerpo se hace incidir sobre un prisma, se descompone en radiaciones monocromáticas cuyo conjunto se denomina “espectro”. Cada radiación monocromática corresponde a una determinada longitud de onda λ, que está relacionada con la velocidad de propagación c por la ecuación: λ = c . T. D0onde T es el período correspondiente al fenómeno periódico al cual responde la radiación.
Por otra parte, T = 1 / υ; siendo υ la frecuencia.
El espectro se puede dividir en tres zonas:
- zona infrarroja: constituida por radiaciones de longitud de onda superiores a 0,8 μ.
- zona luminosa o visible, cuyas radiaciones poseen longitudes de onda comprendidas entre 0,4 y 0,8 μ. e impresionan la retina humana.
- zona ultravioleta, cuyas longitudes de onda son inferiores a 0,4 μ..
La energía radiante es emitida por toda la materia del cuerpo, pero en general, en su interior la energía emitida por cada punto es nuevamente absorbida por eso solamente se libera la energía correspondiente a una delgada capa de la superficie del cuerpo. no solo depende de la temperatura de la superficie sino también de su naturaleza.
Distribución espectral de la energía radiante
Lumer y Pringssheim, efectuaron una serie de experimentos en los cuales tomaban las radiaciones emitidas a una cierta temperatura y medían su energía a distintas longitudes de onda. Así encontraron que la energía en las distintas longitudes de onda no eran uniforme. Si E λes la energía emitida con longitud de onda λ, la energía total a temperatura T está dada por:
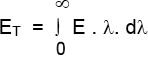
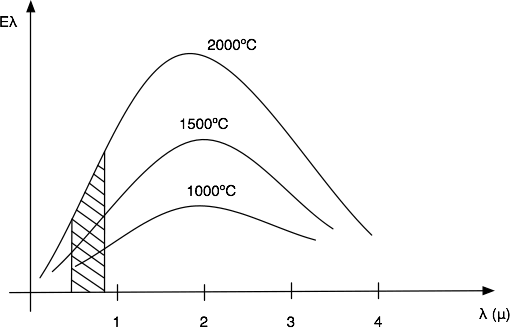
Por lo tanto, el área encerrada por cada curva representa la energía total emitida a esa temperatura, será proporcional a la cantidad de calor transmitida por unidad de superficie y unidad de tiempo.
Se puede observar que a temperaturas bajas, la energía emitida corresponde a radiaciones de longitudes de onda ubicadas en la zona infrarroja. a medida que el cuerpo aumenta su temperatura, emite radiaciones de longitud de onda cada vez menores, alcanzando la zona roja de luz visible y posteriormente al cubrir todo el espectro visible, la luz blanca. Por este motivo, los cuerpos a temperaturas elevadas presentan color rojo y también blanco.
Radiación incandescencia
Hemos visto anteriormente que la energía emitida por un cuerpo depende de su temperatura.
La energía radiante recibida por un cuerpo, en general puede dividirse en tres partes:
a) la energía transmitida o programada por el cuerpo sin absorberla;
b) la energía reflejada o difundida según las leyes de la óptica y
c) la energía que el cuerpo absorbe
La cantidad de energía transmitida, reflejada o absorbida por un cuerpo, depende de la naturaleza del material, de la superficie y de la longitud de onda de la radiación. En realidad no existen cuerpos totalmente permeables o impermeables. Por ejemplo, el vidrio es permeable a las radiaciones visibles pero absorbe las infrarrojas.
Podemos imaginar la existencia de un cuerpo que sea absolutamente absorbente o sea un cuerpo que absorbiera todas las radiaciones que recibe. Un cuerpo teórico que cumple esta condición, se denomina cuerpo negro.
Un cuerpo negro, se puede lograr casi perfectamente practicando un orificio pequeño, de superficie ΔS, en un recinto cerrado, opaco o recubierto de negro de humo, y mantenido a temperatura constante. La radiación absorbida o emitida por dicho sistema, es equivalente a la que correspondería a un cuerpo negro de superficie ΔS, a la misma temperatura. A unos 500 °C, la radiación que emite u cuerpo negro, comienza a tener radiaciones luminosas (rojo cereza). Midiendo la energía de dicha radiación, se puede medir la temperatura del cuerpo, procedimiento en que se basan los métodos ópticos de medición de temperatura en los hornos industriales.
Poder emisivo y poder absorbente
El poder emisivo o de emisión E, de un cuerpo, se define como la cantidad de calor emitida por unidad de superficie y por unidad de tiempo, en una dirección dad. El valor de E depende fundamentalmente del valor de λ y de T. En general se expresa relacionándola con el poder emisivo del cuerpo negro ideal.
Se denomina coeficiente de emisividad e a la relación entre el poder emisivo del cuerpo E, y el poder emisivo del cuerpo negro ES, en iguales condiciones. O sea:
En la expresión anterior vemos que e debe ser un número, independiente de las unidades en que se mida el poder emisivo y cuyo valor está comprendido entre 0 y 1.
Por ejemplo, entre 20 y 200°C, los valores aproximados de e son:
MATERIAL |
e |
|---|---|
metal pulido |
0,04 – 0,05 |
| metal oxidado |
0,80 - 0,90 |
madera lisa |
0,80 - 0,90 |
material de construcción |
0,90 |
vidrio liso |
0,94 |
negro de humo |
0,98 |
El poder absorbente o de absorción A, de un cuerpo, se define como la cantidad de calor absorbida por unidad de superficie y por unidad de tiempo. Su valor depende de λ y T. Se denomina coeficiente de absorción a, a la relación entre el poder absorbente del cuerpo A y el poder absorbente correspondiente al cuerpo negro en las mismas condiciones AS.
valor comprendido entre 0 y 1
Se deduce entonces que tanto aS correspondientes al cuerpo negro ideal, deben valer 1.
Ley de KIRCHOFF
Esta ley establece que la relación entre el poder emisivo y el coeficiente de absorción, es una constante para todas las superficies a valores de λ y de T dados.
Si llamamos E1 y E2 a los poder emisivos de dos cuerpos cuyos coeficientes de absorción son a1 y a2, se deberá cumplir que::
E1 = E2 también igual a 
para el cuerpo negro
Como para el cuerpo negro, aS = 1; entonces el valor de la constante es igual a ES o sea el poder emisivo del cuerpo negro en las condiciones de λ y de T dadas.
Vemos entonces que todo cuerpo puede emitir radiación a una λ y T dadas, según el valor de su coeficiente de absorción.
La radiación será mayor cuanto mayor sea el valor de a, en consecuencia el cuerpo negro es el que mayor radiación emite en tales condiciones, pues su valor de a es máximo, igual a 1.
Según la ley de Kirchoff, para un cuerpo cualquiera, cuyo poder emisivo es E y su coeficiente de absorción es a, se debe cumplir que:
donde ES = poder emisivo del cuerpo negro
Pero, según vimos antes, E = e; donde e es el coeficiente de emisividad del cuerpo, en consecuencia:
donde e = a
Se deduce que para toda superficie, el coeficiente de emisividad es igual al coeficiente de absorción. Por tanto, si un cuerpo puede emitir una radiación λ a temperatura T, el mismo cuerpo es también capaz de absorberla en las mismas condiciones. Este fenómeno se conoce como inversión del espectro.
Resumiendo lo dicho, se puede establecer que la cantidad de calor transmitida por radiación y por unidad de tiempo, depende no solamente de la temperatura y de la naturaleza de la superficie del cuerpo sino también de las temperaturas y naturaleza de las superficies de los cuerpos circundantes.
Cuerpos grises
Son aquellos en los cuales el valor del coeficiente de emisividad e, permanece constante para todas las longitudes de onda y temperaturas. Como vimos que e = a, el coeficiente de absorción también debe ser constante. En la práctica no existen cuerpos grises, pues el valor de e no se mantiene constante, sin embargo, en la mayoría de los casos pueden considerarse grises a los cuerpos sin mucho error.
El poder emisivo de un cuerpo gris será:
E = e . ES
Esta ecuación se considera válida para todas las longitudes de onda y en un intervalo dado de temperatura.
Ley de stefan boltzmann
Establece que la cantidad total de calor emitida (en todas las longitudes de onda), por unidad de tiempo y por unidad de superficie del cuerpo negro, es proporcional a la cuarta potencia de la temperatura absoluta del cuerpo. (Según lo visto antes, la cantidad de calor total emitida es proporcional al área encerrada por la curva de radiación: E λ = f(λ).
Esta ley se puede expresar matemáticamente:
Donde es el coeficiente de radiación total del cuerpo negro, que se puede definir como la radiación integral, para todas las direcciones y longitudes de onda transmitida por unidad de superficie del cuerpo negro, en la unidad de tiempo y por °K de temperatura. Es una constante universal.
Par los cuerpos grises podemos aceptar que:
δQ = σs S dτ T4 para un cuerpo gris : σ = e σs
δQ = e σs S dτ T4 o 
Donde σs = 4,96 x 10-8 Kcal / m2 h ºK4
Calor transmitido por radiación
Supongamos que un cuerpo 1 a temperatura T1 y de superficie S1 transmite calor a otro cuerpo 2 de temperatura T2 y superficie S2, considerando además que el medio que lo rodea no es absorbente. La cantidad de calor transmitida será igual a la cantidad de calor emitida por el cuerpo 1 a temperatura T1 menos la cantidad de calor reflejada por el cuerpo 2 y menos la cantidad de calor emitida por dicho cuerpo a T2 y absorbida por 1.
Si el cuerpo 1 fuera gris y el 2 negro y rodeara totalmente a 1, las cantidades de calor serían:
Ejemplo:
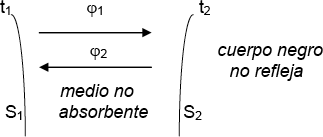
- Calor emitido por 1
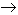ϕ1 = e1 σs S1 T14 - El cuerpo 2 por ser negro no refleja radiación
- El cuerpo 1 absorbe de 2 ϕ2 = e1 σs S1 T24
Calor transmitido: ϕ = ϕ1 - ϕ2 = e1 σs S1 ( T14 - T24 )
Si t = T – 273,15 ϕ = αr S1 ( t1 - t2 )
Donde
αr = se denomina coeficiente de radiación.
Calor transmitido por radiación y convección
Si un cuerpo de temperatura t1 y superficie S1se encuentra dentro de un fluido a temperatura t2, siendo t1 > t2, transmite calor por convección y radiación.
(Si estuviera apoyado, también transmitiría calor por conducción a través de los apoyos). El flujo total, transmitido por convección y radiación, según las ecuaciones ya vistas será:
ϕ = α . S1 (t1 - t2) + αr . S (t1 - t2)
donde α = coeficiente de convección
ϕ = (α + αr ) . S1 (t1 - t2)
BIBLIOGRAFÍA
ZEMANSKY, MARK W.- CALOR Y TERMODINÁMICA. EDIT. AGUILAR S.A 1979
SEARS, FRANCIS W.- TERMODINÁMICA. EDITORIAL REVERTÉ, S.A. 1969
WILSON, JERRY D.- PHYSICS. EDIT.HEAT. SEGUNDA EDICIÓN, 1983
RESNICK Y HALLIDAY.- FISICA, EDITORIAL CECSA, PARTE I, 1990
CEIT, UTN FACULTAD REGIONAL BUENOS AIRES.- APUNTE FISICA II B, CALOR Y TERMODINÁMICA, 1995
FERNÁNDEZ Y GALLONI.- FISICA ELEMENTAL. EDITORIAL NIGAR. BUENOS AIRES.1980