Conducción de calor a través de paredes superpuestas
El caso más general que se presenta en la práctica es la transmisión de calor por conducción a través de paredes de distintos materiales y propiedades transmisoras. Consideremos tres paredes superpuestas cuyas resistencias térmicas son ρ1 , ρ2, ρ3 , limitadas por las superficies isotérmicas de temperaturas t1 , t2 , t3 y t4, siendo t1 > t2 > t3 > t4, las líneas de flujo se dirigen en la dirección que indica la figura.
Conforme a lo visto anteriormente, el flujo que atraviesa la pared de resistencia térmica ρ1, ρ2, y ρ3 será respectivamente:
y para las otras paredes: 
Cuando se ha alcanzado el estado de régimen permanente:
ϕ1 = ϕ2 = ϕ3 = ϕ, entonces ϕ (ρ1 + ρ2 + ρ3 ) = (t1 - t2) + (t2 - t3) + (t3 - t4)
De donde :
Esto significa que el flujo calorífico que atraviesa paredes superpuestas de diferentes materiales es igual a la relación entre la diferencia de las temperaturas extremas y la suma de las resistencias térmicas del material de las paredes.
Conducción del calor a través de diferentes materiales entre dos superficies isotérmicas
Sean dos materiales de resistencias térmicas ρ1 y ρ2 que transmiten calor por conducción entre dos superficies isotérmicas de temperaturas t1 y t2.
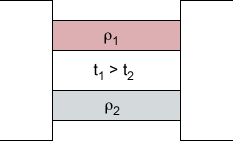
Si t1 > t2, cuando se alcanza el estado térmico de régimen permanente, el flujo que atraviesa t1 > t2 el material de resistencia térmica ρ 1 será:
y para el otro material: 
El flujo total entre las dos superficies isotérmicas será:
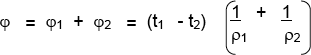
Nota: se puede hacer una analogía entre la corriente eléctrica y las resistencias, cuando se conectan en serie y cuando se conectan en paralelo.
Ecuación general de la conducción de calor en el espacio, en régimen variable
La ecuación de Fourier que hemos visto, está referida al eje de las “x”, sin embargo, si consideramos un cuerpo en el cual se transmite en tres direcciones en el espacio, debemos referirnos a los ejes “x”, “y”, “z”.
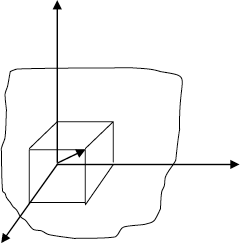
Si tomamos un punto “o” de un sólido en el cual consideramos un paralelepípedo elemental de aristas dx, dy, dz, el flujo que pasa por la cara normal al eje “x”, de superficie dy, dz será de acuerdo a la ley de Fourier:
ϕox = - λ . dy . dz . dT/dx
En estado térmico de régimen variable, la variación de flujo por unidad de camino será
; y para el camino dx : 
; o sea que:
del mismo modo para el eje “y” :
y para el eje z:
Sumando las tres ecuaciones:
Para el cubo elemental: dx . dy . dz = dV, volumen elemental:
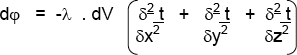
Si consideramos que la variación del flujo provoca una absorción de calor, por la masa del elemento de volumen, como la temperatura aumenta, el segundo miembro de la ecuación anterior será positivo.
Si denominamos δQ al valor elemental absorbido por el elemento de volumen en el tiempo dτ , la variación del flujo en dicho tiempo será:
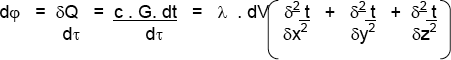
donde, m es la masa del elemento de volumen, o su valor específico y dt la elevación de temperatura producida en el tiempo dτ.
Si llamamos al peso específico del cuerpo 
; G = γ . dV
Reemplazando en el ecuación anterior y simplificando:
de donde
El término entre paréntesis se denomina operador de Laplace o Laplaciano, que se indica con el símbolo ∇2 (delta cuadrado), luego podemos escribir:
La magnitud 
se denomina difusividad térmica “a “ y depende del material, de donde:
Si tomamos el caso particular de régimen estacionario o permanente, como la temperatura no varía con el tiempo: 
; pero como λ ≠ 0 se deberá cumplir que:
∇2. t = 0 ,
condición a cumplir para el estado de régimen estacionario o permanente.
Para el caso del muro, o sea paredes planas y paralelas, como el flujo se transmite sólo en dirección “x”, se deberá cumplir que:
De donde dt = C.dx, e integrando : t = C . x + C’ , o sea que obtenemos una expresión que nos indica que la temperatura varía linealmente con la dirección del flujo, lo cual ya habíamos aplicado al definir gradiente o caída de temperatura.