Habíamos definido que el calor se transmite por convección en el caso de los fluidos: gases o líquidos, cuando absorben calor en una porción y luego esta porción se desplaza mezclándose con otra más fría cediéndole calor. Este movimiento se denomina corriente de convección y si es provocado por diferencias de densidad debidas a diferencias de temperatura, tenemos, el fenómeno de convección natural.
Si, en cambio, el movimiento del fluido se efectúa por medio de un agitador, una bomba o un ventilador, corresponde a la convección forzada.
Cuando un fluido está en contacto con una pared sólida de mayor temperatura, aunque el fluido se encuentra en movimiento turbulento, se forma junto a la pared una película de fluido. Cuanto más turbulenta sea el movimiento, más delgada es la película, también llamada capa límite. El fenómeno de transmisión de calor de la pared al fluido se realiza por conducción a través de la película y a la vez por convección del fluido. En conjunto, el fenómeno es complejo porque la cantidad de calor transmitida dependerá de varios factores concurrentes: como ser la naturaleza del fluido ; el estado del fluido (densidad, viscosidad, calor específico y conductibilidad térmica); de la velocidad del fluido (si es mínima, el movimiento será laminar y si es considerable, turbulento); de que el intercambio de calor provoque evaporación, condensación o formación de la película; de la forma del sólido (pared plana o curva, vertical u horizontal); de la naturaleza de la superficie (rugosa o lisa) y de que el sólido sea buen o mal conductor.
La cantidad de calor transmitida por convección se expresa por la Ley de Newton:
δϕ = α S dt dτ
En esta expresión empírica, α se denomina coeficiente de convección, coeficiente pelicular o coeficiente de conductibilidad exterior, y se puede definir como la cantidad de calor que se transmite a través de la unidad de superficie de separación entre el sólido y el fluido, cuando la diferencia de temperatura entre ambos es unitaria y en la unidad de tiempo. El coeficiente pelicular tiene en cuenta todas las variables enunciadas anteriormente por lo que el problema fundamental de la transmisión de calor por convección es encontrar el valor que resulte apropiado para cada caso en particular. Su valor en el sistema técnico oscila entre unas pocas unidades (aire casi quieto) y más de 10.000 (vapor saturado que se condensa).
Unidades de α: si despejamos en la expresión de Newton: ![]()
En el sistema SI.: ![]() o bien
o bien ![]()
en el técnico: ![]()
y en el c.g.s. ![]()
Consideraciones generales sobre los coeficientes peliculares
Para calcular el valor de α se puede proceder en forma teórica o experimental. En esta última forma, los resultados se deberán aplicar solamente a casos análogos a las experiencias realizadas. Las ecuaciones que sean utilizadas para determinar α deberán incluir todas las propiedades del fluido en particular y las condiciones de su movimiento.
En forma teórica, uno de los métodos más útiles encontrados hasta ahora y que permite relacionar todos los factores que intervienen en la convección es el análisis dimensional, también llamados modelos de similitud. En este método, las variables se vinculan y ordenan en grupos adimensionales, o sea relaciones numéricas sin unidades o dimensiones.
Los grupos más importantes que se han determinado son:
Número de Grashof: ![]()
Número de Nusselt: ![]()
Número de Prandtl: ![]()
Número de Reynolds: ![]()
Donde: α es el coeficiente pelicular, D las dimensiones lineales del recinto (por ejemplo el diámetro o longitud de una cañería), λ el coeficiente de conductibilidad, ω la velocidad lineal del fluido, η su viscosidad, c el calor específico, δ la densidad, g la aceleración de la gravedad, β el coeficiente de dilatación cúbica y Δt , la diferencia de temperatura.
El número de Reynolds contiene la velocidad del fluido, por lo tanto medirá su grado de turbulencia y será importante en el caso de la convección forzada cuando los fluidos posean movimiento turbulento. El número de Grashof incluye el coeficiente de dilatación y la fuerza ascensional provocada por la variación de temperatura, proporcional a g. β . Δt; en consecuencia el Gr mide el grado de convección natural. Su valor en cambio es despreciable en la convección forzada. Por el contrario, el Re en la convección natural desaparece pues la turbulencia es pequeña debido a la baja velocidad. El número de Prandtl contiene únicamente las propiedades del fluido o sea que dependerá solamente de su naturaleza.
En el caso de los gases, la viscosidad η es tan pequeña que Pr se puede considerar despreciable. Por lo tanto resumiendo:
En los gases
Convección natural: Nu, Gr
Convección forzada: Nu, Re
Y en los líquidos
Convección natural : Nu, Gr, Pr
Convección forzada: Nu, Re, Pr
En el caso más general, se encuentra que la ecuación que vincula los números adimensionales es de la forma:
Nu = f ( Re, Pr, Gr)
Aunque esta función puede tomar la forma de cualquiera de las conocidas, se simplifica suponiendo que cada número entra en la ecuación una sola vez y como función de potencia. Esta suposición se cumple aproximadamente en la mayoría de los casos prácticos. Podemos entonces escribir:
Nu = K Rea , Prb , Grc
donde K, a, b y c son constantes que se deben determinar experimentalmente

Para ello se puede encontrar experimentalmente la variación
del Nu con Re y Gr en cada caso en particular y luego
trazar en un diagrama dicha variación tomando en
ordenadas y en abscisas los logaritmos de los valores encontrados.
En efecto, tomando logaritmos se cumple que:
log Nu = log K + a log Re + b log Pr + c log Gr
El coeficiente angular de las rectas encontradas nos dará el exponente correspondiente a cada número. El término independiente corresponde al valor del long K. Una vez conocidas las constantes, se puede calcular el coeficiente pelicular α despejándolo del número de Nusselt:
![]()
Transmisión del calor por conducción y convección
Uno de los casos más frecuentes en la práctica es la transmisión de calor entre sólidos y fluidos, o sea la transmisión mediante la conducción y convección combinadas.
Consideraremos una pared sólida que separa dos fluidos, uno de los cuales calienta al otro trazamos en ordenadas el eje correspondiente a las caídas de temperaturas producidas en la pared y cada una de las películas.
Llamaremos t1 la temperatura del fluido caliente y su coeficiente pelicular, t la temperatura del fluido frío y su coeficiente pelicular; es el coeficiente de conductibilidad del material de la pared y e su espesor ( t > t ).
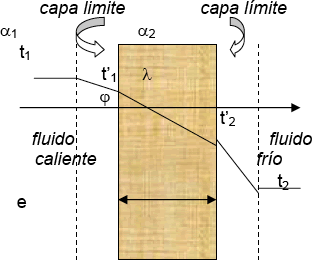
Cuando se ha alcanzado el estado térmico de régimen permanente, el flujo que atraviesa la película de coeficiente por unidad de superficie será:
δQ = α S dτ dt
![]() Ley de Newton
Ley de Newton
![]() Ley de Fourier
Ley de Fourier
![]() Ley de Newton
Ley de Newton
Sumando miembro a miembro
![]()
Si hacemos : . 1 . = K
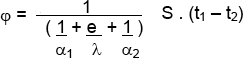
![]()
ϕ = K . S . Δt
El coeficiente K se denomina coeficiente de transmisión de calor total, y se lo puede definir como la cantidad de calor que en la unidad de tiempo atraviesa la unidad de superficie de pared interpuesta entre dos fluidos, cuando la diferencia de temperatura entre ambos fluidos es unitaria.
las unidades de K serán;
![]()
ó bien
![]()
Diferencia variable de temperaturas
La ecuación anterior es aplicable cuando la diferencia de temperatura entre los fluidos permanece constante. Sin embargo, en los aparatos utilizados para intercambio de calor, la temperatura de los fluidos varía con la superficie de intercambio.
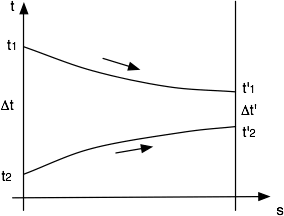
Tomemos por ejemplo el caso de un refrigerante de laboratorio. Es evidente que podemos hacer circular los fluidos en dos formas distintas. En el primer caso los dos fluidos penetran por el mismo extremo del intercambiador. Este caso se denomina de corrientes paralelas o equicorrientes. En el segundo caso, los fluidos penetran por los extremos opuestos del intercambiador y se denomina de contracorriente.
En el caso de corrientes paralelas, el fluido caliente se enfría desde t a t’ (ver diagrama y figura I), mientras que el fluido frío se calienta desde t a t’.
En el caso de contracorriente, en cambio, el fluido frío se calienta desde t’ a t (ver diagrama y figura II).
Se puede observar que el salto o diferencia de temperaturas t varía en ambos casos entre t y t’ a lo largo de la superficie de intercambio, en consecuencia podremos aplicar la ecuación de transmisión de calor total siempre que conozcamos la diferencia media de temperatura entre dichos límites. Se puede demostrar que la diferencia media de temperatura responde al promedio logarítmico dado por la ecuación:
Si Δt = cte. entre los fluidos ![]() ϕ = K . S . Δt
ϕ = K . S . Δt
Si Δt ≠ cte. ![]()
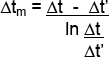
en consecuencia ϕ = K . S . Δtm
Corrientes paralelas o de igual sentido
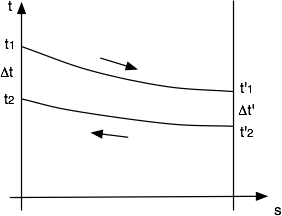
Corriente de sentido contrario o contracorriente