Para comprender la dilatación, es conveniente visualizar el fenómeno a nivel microscópico, la expansión térmica de un sólido sugiere un aumento en la separación promedio entre los átomos en el sólido. La curva de energía potencial de átomos contiguos en un sólido cristalino, en función de su separación internuclear, es de trazado asimétrico, como la que se indica en la Figura 3.3. Conforme los átomos se van aproximando, su separación disminuye respecto del valor de equilibrio ro, entonces intervienen fuerzas repulsivas intensas y la curva de potencial aumenta rápidamente, recordemos que el valor de dicha fuerza está dado por la expresión: F = - dU/dr. Conforme los átomos se alejan, sus separaciones aumentan respecto del valor de equilibrio y entonces intervienen fuerzas un tanto más débiles y la curva de potencial aumenta de una manera más lenta. Para una energía vibracional dada, la separación de los átomos cambiará periódicamente de un valor mínimo a uno máximo y la separación promedio será mayor que la separación de equilibrio, debido a la naturaleza asimétrica de la curva de energía potencial. Cuando la energía vibracional es mayor aún, la separación promedio será también más grande. El efecto es aumentado por el hecho de que al tomar el promedio temporal del movimiento, se debe tomar en cuenta el mayor tiempo transcurrido en las separaciones extremas (en donde la rapidez vibracional es menor). Debido a que la energía vibracional aumenta conforme lo hace la temperatura, la separación promedio entre los átomos aumenta con la temperatura y el sólido como un todo se expande. Recordemos, que la energía potencial molecular, se puede expresar como la suma de las energías cinética media, rotacional y vibracional:
Em = Ekmed + Er + Ev,
Donde Ekmed, representa la energía cinética media, Er, la energía rotacional, y Ev la energía vibracional.
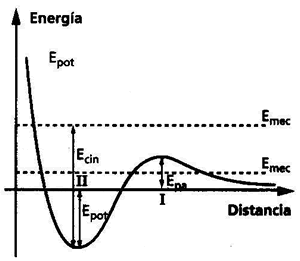
figura 3.3
Debemos hacer notar que si la curva de Energía potencial fuese simétrica en torno a la separación de equilibrio, la separación promedio correspondería a la separación de equilibrio, sin importar que tan grande fuese la amplitud de la vibración. Por lo tanto, la expansión térmica es una consecuencia directa de la desviación de la simetría (es decir, de la asimetría) de la curva de energía potencial característica de los sólidos.
Algunos sólidos cristalinos pueden contraerse, en ciertas regiones de temperatura, conforme la temperatura aumenta. El análisis anterior sigue siendo válido sólo si se supone que únicamente existen modos de vibración compresional, (es decir, longitudinales) y que esos modos son predominantes. Sin embargo, los sólidos pueden vibrar en modos transversales (es decir, cortantes) al igual que en modos vibracionales y esto permiten que el sólido se contraiga con los aumentos de la temperatura, disminuyendo con ello la separación promedio de los planos atómicos. En ciertos tipos de estructura cristalina, y en ciertas regiones de temperatura, estos modos transversales de vibración pueden predominar sobre los longitudinales, dando lugar a un coeficiente de expansión térmica total negativo.
Existe por lo tanto una relación directa entre las fases y la estructura molecular, o dicho de otro modo una relación directa entre el estado de agregación y la energía potencial molecular, y como consecuencia también entre la energía vibracional y la dilatación.
Físicamente tiene importancia esta relación entre el coeficiente de expansión o dilatación con la estructura atómica o molecular. Debemos aclarar que los modelos microscópicos presentados son una sobresimplificación de un fenómeno mucho más complejo, que puede tratarse con mayor detalle al relacionar la termodinámica y la teoría cuántica.

figura 3.4 Imagen fotográfica de una misma regla graduada a diferentes temperaturas ta < tb
El cambio porcentual de la longitud de muchos sólidos, llamados isotrópicos, asociados con un cambio dado de la temperatura, es el mismo sobre cualquier línea del sólido. La dilatación es totalmente análoga a una amplificación fotográfica, excepto en que el sólido es tridimensional. Si tenemos una lámina delgada en la que se practica un orificio, el cambio ΔL / L = αΔΤ para una ΔT dada es el mismo para la longitud, el espesor, la diagonal de una cara, la diagonal del cuerpo y el diámetro del orificio. Cualquier línea, sea recta o curva, se alarga en la relación α por aumento de un grado de temperatura. Si se escribe un nombre rayando la lámina, la línea que representa dicho nombre tiene el mismo cambio fraccional de longitud que cualquier otra línea. En la Figura 3.4 se muestra la analogía con una amplificación fotográfica. Si observamos la regla de acero de la Figura 3.4, a dos temperaturas diferentes, la regla a) a una temperatura to y la regla b) a una temperatura t1, tal, que t1 > to. En la dilatación, todas las dimensiones aumentan en la misma proporción: la escala, los números, el orificio y el espesor aumentan todos en el mismo factor, (la dilatación mostrada, está obviamente exagerada, ya que correspondería a un aumento imaginario de unos 100 000 ºC en la temperatura. Teniendo en cuenta estas ideas, podríamos demostrar con un alto grado de precisión, que el cambio fraccional en el área A por cada cambio de un grado en la temperatura en un sólido isotópico es 2α, es decir:
ΔA = 2α. A.Δt, [3.7]
y que el cambio fraccional en volumen V por cada cambio de un grado de temperatura en un cuerpo isotrópico es 3α, es decir,
ΔV= 3α.V.Δt [3.8]