Dilatación superficial

Cuando tomamos un plano dentro de un cuerpo sólido, de modo que el área de la superficie de dicho plano esta dada por la expresión: S = L₁.L₂, se determina que:

S_t = S_o ( 1 +2α.t), [3.13]

Con ( 1 +2α. t) llamado binomio de dilatación superficial

Si S = L₁.L₂

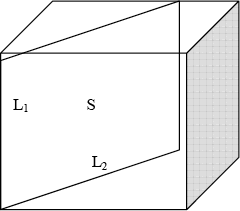
figura 3.6

derivando a S respecto de t:

dividimos m.a. m. por S

queda:

Observando el segundo miembro se puede establecer que:

         dS = 2α .S.dt

Integrando entre S_o y S_t

Por ser isótropo α₁=α₂=α

S_t = S_o ( 1 +2α t), [3.14]

con ( 1 + 2α. t) como binomio de dilatación superficial.

(Como ejercitación se propone demostrar para un sólido, ΔV = 3αV_oΔΤ, tal que el coeficiente de dilatación volumétrico β = 3 α_L)