La Estructura Cristalina

Un sólido cristalino, o cristal, es una ordenación periódica de estructuras idénticas. La estructura idéntica que se repite, recibe el nombre de base cristalina. La estructura sobre la que se repite, el de red cristalina, (Fig.1.1).

Tres vectores, a, b y c definen una red cristalina a través de tres enteros n₁, n₂y n₃, de modo que si es el vector de posición de un punto de la red, el expresado por:

(1.1)

también lo es. El vector

(1.2)

define el grupo de traslaciones del cristal.

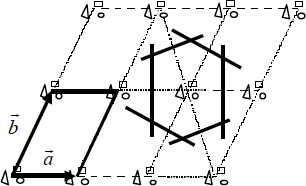
Figura 1.1.- Cristal, celdilla primitiva y celdilla de Wigner- Seitz en dos dimensiones

En toda red cristalina se pueden encontrar (y no de forma única) tres vectores de forma que dos puntos reticulares cualesquiera están siempre relacionados por una expresión del tipo (1.1) con n₁, n₂y n₃ enteros. Los vectores a, b y c que cumplen también esto, definen una celdilla que también por traslación genera el cristal. Se la llama celdilla primitiva porque es la de volumen mínimo que por traslación reproduce el cristal. Si hubiera otra de menor volumen y tomando n₁, n₂y n₃ enteros, no encontraríamos necesariamente un punto reticular (Fig. 1.1). Es fácil comprender que a cada celdilla primitiva le corresponde un solo punto reticular (con su correspondiente base cristalina).

La celdilla primitiva no es única. Una forma de concretar la celdilla primitiva es bisecar por planos los segmentos que unen un punto reticular a sus próximos vecinos. En este caso recibe el nombre de celdilla elemental de Wigner-Seitz (Fig. 1.1) y cumple con los postulados anteriores. En particular, es evidente que sólo contiene un punto reticular.

Las redes cristalinas se llaman también redes de Bravais y hay 14 diferentes agrupadas en 7 sistemas cris talinos (Fig. 1.2).

Sistema	Redes	Malla	Redes de Bravais
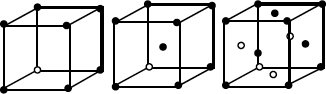
Cúbico	Simple Centrado en cuerpo Centrado en caras	a = b = c α = β = γ = 90º
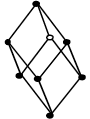
Trigonal	Romboédrico	a = b = c α = β = γ ≠ 90º
Hexagonal	Simple	a = b ≠ c α = β = 90º γ ≠ 120º
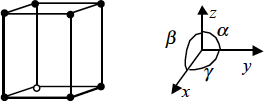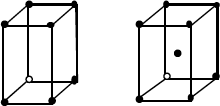
Tetragonal	Simple Centrado en cuerpo	a = b ≠ c α = β = γ = 90º
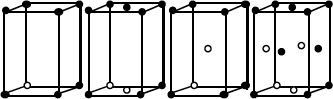
Ortorrómbico	Simple Centrado en bases Centrado en cuerpo Centrado en caras	a ≠ b ≠ c α = β = γ = 90º
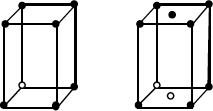
Monoclínico	Simple Centrado en bases	a ≠ b ≠ c α = β = 90º ≠ γ
Triclínico	Simple	a ≠ b ≠ c α ≠ β ≠ γ

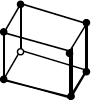Figura 1.2.- Propiedades de las redes de Bravais

De ellos el sistema cúbico es el de máxima simetría y además el sistema de los semiconductores usuales. Más concretamente estos cristalizan en el sistema cúbico centrado en caras (fcc) que puede verse en la Figura 1.2. Tienen asociada, normalmente, una base cristalina de dos átomos que pueden ser iguales (como en los semiconductores elementales: Silicio, Germanio…) o diferentes (Arseniuro de Galio, Fosfuro de Indio y otros semiconductores formados por asociación de elementos de los grupos III y V, o II y VI del sistema periódico). Para este caso se representa en la Fig. 1.3 la estructura atómica de un material diatómico (tipo blenda, que es la estructura cúbica del SZn). Es fácil ver que los átomos "blancos" marcan la estructura fcc y que cada átomo blanco tiene asociado otro "negro". Cuando todos los átomos son iguales tenemos el caso de las estructuras del tipo diamante.

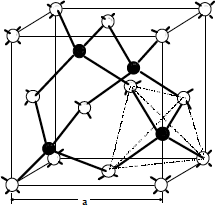
Figura 1.3.- Estructura diatómica fcc

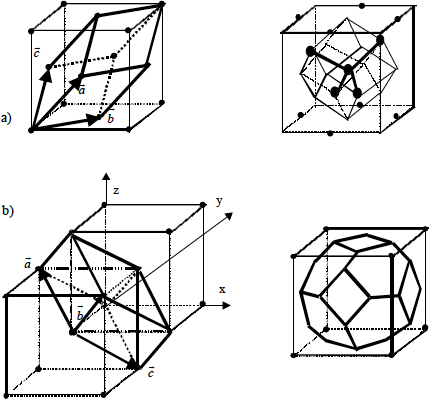
Figura 1.4.- Vectores primitivos de la red fcc (a) y bcc (b).
Respectivas celdillas de Wigner-Seitz.

 

Puede verse que esta estructura es compatible con enlaces de tipo tetraédrico, típico de los enlaces covalentes entre orbitales sp³. Una celdilla primitiva puede ser un romboedro, mientras que la celdilla de Wigner-Seitz es un dodecaedro rómbico regular (Fig.1.4). En la Tabla 1.1 se dan los parámetros de red (lado del cubo del sistema) para algunos semiconductores usuales.

TABLA 1.1.- Parámetros de red de semiconductores fcc

Semiconductor	a (Å)	Semiconductor	a (Å)
Diamante	3.6680	GaP	5.4504
SiC - (3C)	4.3596	GaAs	5.6533
Si	5.4307	InAs	6.0584
Ge	5.6575	InP	5.8688

Algunos semiconductores de interés actual cristalizan en el sistema hexagonal. Son semiconductores que presentan enlaces de tipo tetraédrico, semejantes a los del Silicio. En la Figura 1.5a se representa este tipo de estructura, que se conoce con el nombre de Wurtzita (que es la forma hexagonal del sulfuro de zinc, SZn.). La estructura puede obtenerse a partir de prismas de base rómbica, de 60º de ángulo.

Normalmente se le asocian cuatro ejes: a₁ , a₂ y a₃ , que forman entre sí ángulos de 120º y un cuarto eje, c , normal a los anteriores. Puede observarse, también, que la red hexagonal procede del empaquetamiento compacto. La formación de este tipo de estructura puede imaginarse a partir de la colocación de diferentes capas de bolas en una caja: cada bola de una capa es tangente a seis de la misma capa, se apoya en tres de la capa inferior y, con otras dos de su capa, soporta una bola de la superior. Según la posición relativa de las diferentes capas (secuencia de deposición) pueden obtenerse diferentes redes hexagonales y una cúbica centrada en caras, coincidiendo el eje cr con la dirección (1,1,1). Con la periodicidad según cr , reciben diversos nombres: 2H, 3C, 4H, 6H ... .

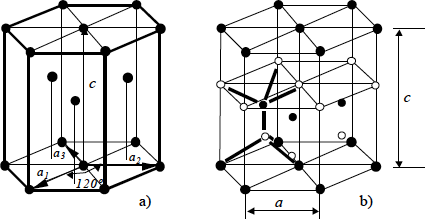
Figura 1.5.- Red hexagonal : a) Estructura cristalina y b) estructura atómica (enlaces tetraédricos)

1.2.- LA RED RECÍPROCA

Para cada cristal su red de Bravais constituye la red directa. Asociada a ella existe la red recíproca.

Dados tres vectores (primitivos) de la red directa se obtienen los tres vectores base de la red recíproca por las relaciones:

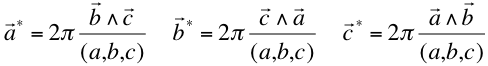(1.3)

que verifican

(1.4)

donde δ_ij es la delta de Krönecker, que toma el valor 1 cuando los dos subíndices son iguales y 0 en todos los demás.

Como ejemplo puede comprobarse que la red recíproca de una cúbica centrada en caras, es otra centrada en el cuerpo y viceversa (Fig. 1.4). También la red recíproca admite varias celdillas primitivas. Entre ellas es posible construir la de Wigner-Seitz, que en este caso recibe el nombre de 1ª Zona de Brillouin.

1.3.- PROPIEDADES DE LA RED RECÍPROCA: ÍNDICES DE MILLER

Sea T* r un vector de traslación de la red recíproca, que expresamos en la forma

con m1, m2 y m3 enteros.

Sea T_N un vector de traslación de la red directa que expresamos en la forma (1.2)

Entonces:

1.3.1.- Familias de planos y direcciones.

El producto

, de acuerdo con (1.4), vale

siendo N, evidentemente, un número entero.

Para cada valor del producto , y dado un vector T* , existen infinitos vectores , cuya proyección sobre es la misma, que cumplen que y cuyas componentes son raíces de la ecuación diofántica:

En la Fig. 1.6 se representa una interpretación geométrica (bidimensional) de este hecho en la que se ha tomado el origen en un punto reticular. Con esta condición los vectores definen puntos reticulares contenidos en un plano que es normal a .

, para todos los valores enteros de N, define una dirección en el cristal [m₁, m₂, m₃] y una familia de planos reticulares normales a ella (m₁, m₂, m₃).

1.3.2.- Distancias entre planos de la familia

Si m₁, m₂, m₃ no tienen factores comunes, dos valores consecutivos de N (N y N+1) definen dos planos consecutivos de la familia y la distancia, d, entre ellos será tal que

es decir:

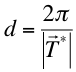(1.5)

siendo y vectores de los puntos reticulares de los planos correspondientes a N y N+1.,

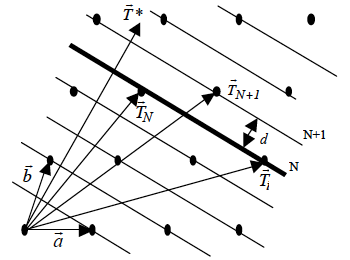
Figura 1.6.- Planos reticulares e índices de Miller

1.3.3.- Casos particulares: Índices de Miller

Es interesante ver cual es la intersección de la familia de planos sobre los ejes. Si la familia interseca a los ejes ar,br y cr con intervalos d₁, d₂ y d₃ (Fig. 1.5), medidos cuando se toma como unidad , , , respectivamente, se tendrá que:

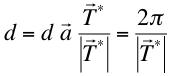
o sea:

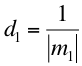
ya que ; y así también para b y c.

Es decir, la familia de planos interseca a los ejes a distancias proporcionales a 1/m₁, 1/m₂ y 1/m₃ (en términos del espaciado de la red).

Dicho de otra forma m₁, m₂ y m₃ son proporcionales a los inversos de las mencionadas distancias.

Si además se escogen los menores posibles (es decir, sin factores comunes), verifican (1.5) y, desde luego, definen una dirección y una familia de planos.

Además, se llaman índices de Miller, que se suelen denotar ordinariamente por (h,k,l). Este símb olo también indica la familia de planos, mientras que [h,k,l] precisa una dirección en el cristal.

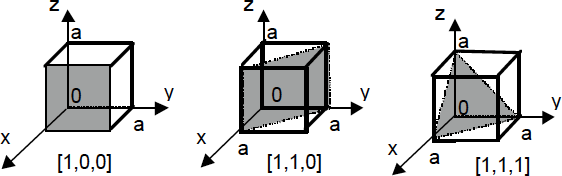
Figura 1.7.- Índices de Miller en una red cúbica.

Un signo - sobre un índice indica que la intersección se ha verificado en el sentido negativo del eje.

Se usan también los símbolos:

{h,k,l} para indicar los planos de simetría equivalentes y

<h,k,l> para indicar las direcciones equivalentes.

Por ejemplo <h,k,l> [0,1,0], [0,0,1], [1,0,0].

En la Fig. 1.7 se representan los índices de Miller más usados y que corresponden a una red cúbica simple.

Para la red hexagonal de la Figura 1.5 y por excepción, al emplear cuatro ejes, los índices de Miller no son tres, sino cuatro. El eje c marca la dirección [0,0,0,1].