Experimento del tapón poroso.
El experimento consiste en dejar fluir un gas desde una presión elevada a otra presión inferior, a través de un tubo que contiene un “estrangulamiento” u obstáculo que puede ser un tapón poroso, una válvula apenas abierta, un orificio muy pequeño, etc. Debido al estrangulamiento, la expansión es muy lenta de tal forma que las presiones a cada lado del obstáculo se mantienen prácticamente constantes.
Se impide el intercambio de calor entre el gas y el medio exterior mediante un aislamiento térmico, de modo tal que el proceso se realice en condiciones adiabáticas.
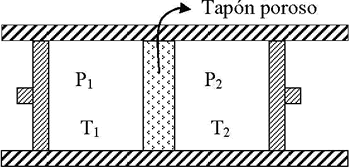
Supongamos, como observamos en la figura, que el gas fluye por un tubo horizontal, aislado adiabáticamente, que contiene un obstáculo. A un lado del obstáculo se mantiene la presión mayor P1, constante mediante una bomba, y al otro lado una presión menor P2. Esta presión P2 en muchos casos puede ser la presión del medio exterior, por ejemplo la presión atmosférica.
Las temperaturas a las presiones P1 y P2 son respectivamente T1 y T2.
Aplicando la ecuación del Primer Principio para sistemas abiertos, que ya vimos en el tema anterior:
Debido a que el gas fluye lentamente ω1 y ω2 son prácticamente nulos, y ω12/2 y ω22/2 ≅ 0. Como el tubo es horizontal h1 ≅ h2. Además, por estar el sistema aislado adiabáticamente,
Q = 0. Por último, no hay trabajo de circulación, Wc= 2
En consecuencia resulta que U1 + P1 . v1 = U2 + P2 . v2 y por definición de entalpía: H1 = H2.
Este resultado nos indica que el valor de la entalpía es el mismo antes y después del proceso de estrangulamiento. Sin embargo como el proceso es irreversible, y por consiguiente no se conocen los estados intermedios, no se puede decir que la transformación se realice a entalpía constante. Es entonces conveniente aclarar que el proceso de Joule-Thomson no es una transformación isoentálpica, entendiéndose por transformación isoentálpica el lugar geométrico de todos los puntos que representan “estados de equilibrio” de la misma entalpía. No obstante, como la entalpía es una función de estado, en un proceso de estrangulamiento entre dos estados, se cumple que ΔH = 0 y si la transformación es elemental, dH = 0.
Coeficiente de Joule-Thomson.
Si hacemos H=f(P,T), como la entalpía es una función de estado, en un proceso elemental se cumple:
En un proceso de Joule-Thomson: dH=0 por lo tanto:
Haciendo pasaje de términos e indicando con el subíndice H que en el proceso la entalpía inicial y final es la misma:
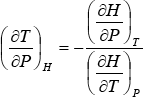
La cantidad 
, que representa la variación de la temperatura con la presión en un proceso de Loule-Thomson, se denomina “coeficiente de Joule-Thomson” y se lo simboliza con la letra μ. Como en la ecuación anterior 
es igual a CP, nos queda finalmente:
(36)
Como H=U + P.V la expresión puede también tomar la forma:
(37)
Que nos da una ecuación completamente general, aplicable a cualquier gas.
En el caso particular de un gas ideal, se cumple que:
en consecuencia, como CP ≠ 0 resulta μ =0
Que nos indica que si un gas ideal sufre un estrangulamiento, su temperatura varía, pues:
Valores y signos del coeficiente de Joule-Thomson
En la ecuación (37) se puede observa que el signo de μ dependerá de los signos y de los valores que toman las cantidades
y 
El signo de 
es generalmente negativo y su valor aproximadamente independiente de la presión.
El término 
a temperaturas ordinarias, es negativo a presiones bajas (excepto el hidrógeno y el helio) y positivo a presiones elevadas.
Como a presiones bajas los dos términos son negativos, μ siendo Cp siempre positivo, el coeficiente de Joule-Thomson, μ será positivo, ecuación (37).
A presiones bajas será entonces positivo el signo de 
Ecuación (36) esto significa que la mayor parte de los gases, (excepto hidrógeno y helio) experimentan un descenso de temperatura cuando sufren una expansión a través de un estrangulamiento, a presiones bajas.
A medida que se eleva la presión, el valor de 
se mantiene aproximadamente constante (negativo), pero el valor de 
disminuye en valor absoluto y a cierta presión se hace positivo, y aumenta en valor absoluto.
Esto significa que a una presión suficientemente elevada, el coeficiente de Joule-Thomson tomará el valor cero y luego se hará positivo, o sea que se producirá la inversión del efecto Joule-Thomson y en estas condiciones, como μ es negativo, la expansión del gas a través del estrangulamiento se producirá con aumento de temperatura. La temperatura a la cual el coeficiente de Joule-Thomson cambia de signo, a una presión dada, se denomina temperatura de inversión. A la temperatura de inversión, el valor de μ debe ser cero.
Aplicación del efecto de Joule-Thomson.
Hemos visto que cuando un gas sufre una expansión a través de un obstáculo o estrangulamiento, a presiones y temperaturas adecuadas, se produce una disminución de su temperatura. Como se cumple que cuanto más baja es la temperatura, el término es de mayor valor absoluto y negativo el coeficiente de Joule-Thomson tendrá los valores positivos más altos, a temperatura bajas.
Como consecuencia de ello, el enfriamiento por efecto de Joule-Thomson será mas pronunciado a temperaturas bajas y presiones bajas.
Este comportamiento se aplica en la industria para licuar un gas, por ejemplo, el aire. Para ello primero se enfría el gas ya sea por contacto con otro más frío o por expansión adiabática, y luego se lo deja expandir a través de un estrangulamiento. La disminución de presión y el descenso de temperatura provocado por este efecto, produce la licuación del gas.