Ya hemos visto que el calor es una forma de energía que se transmite de un cuerpo a otro debido a una diferencia de temperatura entre ellos. Hasta principios del siglo XIX se suponía que en todos los cuerpos existía una sustancia llamada “calórico”, en mayor cantidad cuanto más elevada era su temperatura. Se creía entonces, que al poner en contacto dos cuerpos de diferentes temperaturas, el de temperatura más elevada o sea el de mayor contenido calórico, cedía una parte de tal sustancia al de menor contenido calórico y ambos cuerpos alcanzaban la misma temperatura. Si bien esta teoría explicaba algunos procesos como la conducción del calor, o las mezclas en un calorímetro, algunos hechos experimentales la contradecían. Si el calor fuera una sustancia contenida en su sistema, no sería posible extraerla indefinidamente sin que el sistema no cambie. Por ej, si dentro de un recipiente con agua se hace trabajar un agitador, podemos obtener del agua una cantidad indefinida de calor poniéndola en contacto con un sistema más frío, sin que el agua sufra ningún cambio. Esto demuestra entonces, que el calor no es nada más que una forma de energía, que se transmite cuando existe una diferencia de temperatura, y que se produce a partir de otra forma de energía que desaparece, como lo establece el primer principio.
Análogamente, el trabajo no es algo que pueda estar contenido en un sistema en cantidad definida. La experiencia indica que es posible aplicar una cantidad indefinida de trabajo a un sistema sin que sufra ningún cambio. Lo mismo que el calor, el trabajo requiere una transmisión de energía, con la diferencia que no interviene directamente una diferencia de temperatura.
Podríamos entonces distinguir al calor del trabajo diciendo que son dos formas de energía que se transmiten de un sistema a otro, el primero por diferencia de temperatura y el segundo sin que intervenga directamente una diferencia de temperatura.
Por todo lo expuesto resulta evidente que no tiene sentido hablar de “calor contenido en un sistema”, o “trabajo contenido en un sistema”. Tanto el trabajo como el calor no están asociados al sistema en sí sino a los procesos que pueden provenir de la interacción entre sistema y medio exterior. Debe entonces entenderse que sólo tendrá sentido referirse a un “calor intercambiado” (entregado o extraído al sistema) o bien a un trabajo realizado “por” o “sobre” el sistema.
En el estudio entre las interacciones entre el sistema y su medio ambiente, donde intervienen cambios de energía como calor y trabajo, es importante establecer cuales son los límites del sistema y del medio ambiente. Veamos un ejemplo:
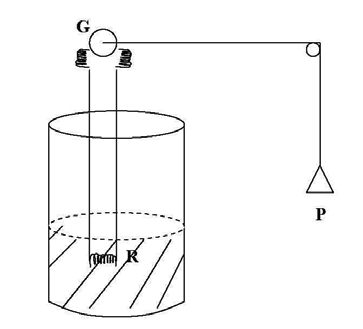
En la figura se muestra un recipiente conteniendo en su interior agua, y dentro del agua una resistencia eléctrica proveniente de un generador G, el cual es accionado por un peso que cae P. Si consideramos que el sistema está formado por el circuito Eléctrico, la resistencia, el agua y el recipiente, experimentalmente se observa que el peso al caer provoca un cambio en el sistema, (elevación de temperatura del conjunto). Como en este proceso no intervienen directamente diferencias de temperatura entre el sistema y medio ambiente que contiene las pesas, el cambio se habrá producido por un trabajo exterior realizado sobre el sistema (pesas que caen).
Si se toma como sistema sólo el agua y el recipiente y el medio ambiente lo forma la resistencia, el circuito eléctrico y las pesas que caen, la diferencia de temperatura entre la resistencia y el agua, provocará una transferencia de calor del medio ambiente al sistema, es decir que sobre éste no se realiza directamente trabajo exterior. Vemos entonces que establecer los límites del sistema y su medio ambiente tiene importancia para determinar la causa que provoca el cambio de estado del sistema, si el flujo de calor, el trabajo exterior o ambas formas de energía a la vez.
Trabajo exterior
Se puede definir como trabajo exterior realizado por o sobre el sistema, a todo desplazamiento sufrido por éste contra o por la acción de fuerzas exteriores (del medio ambiente exterior). En Termodinámica, por convención, se da el signo positivo al trabajo realizado por el sistema sobre el medio exterior y el signo negativo al trabajo realizado sobre el sistema por el medio exterior. En adelante, al trabajo exterior lo simbolizaremos con W.
Trabajo de expansión
Estudiaremos el trabajo exterior que pueden realizar los sistemas denominados “termoelásticos”, o sea lo que pueden sufrir variaciones de volumen, por ej, los gases.
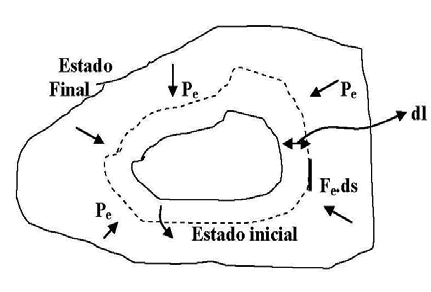
Supongamos que un sistema gaseoso cerrado, se halla sometido a una presión exterior Pe que estimaremos uniforme sobre toda la superficie que limita el sistema. Sobre un elemento infinitamente pequeño ds, la presión ejercida también será Pe.
Si llamamos Fe a la fuerza ejercida por el medio exterior en dirección normal al elemento de superficie, se deberá cumplir que:
Fe = Pe . ds
Si el sistema sufre una expansión infinitesimal hasta un volumen mayor infinitamente
próximo al inicial (línea punteada), el elemento de superficie habrá sufrido un
desplazamiento en dirección normal que llamaremos dl. El trabajo realizado por el
sistema será entonces:
δWe = Fe.dl = Pe.ds.dl
Donde δWe representa el trabajo elemental de expansión realizado por el sistema. Como ds. dl = dv , es decir el volumen infinitesimal en que se ha incrementado el sistema,
δWe = Pe . dv (1)
Si el sistema sufre una expansión desde un estado inicial de volumen vi, hasta un estado final vf, el trabajo de expansión realizado por el sistema en la transformación de i a f será:
![]() (2)
(2)
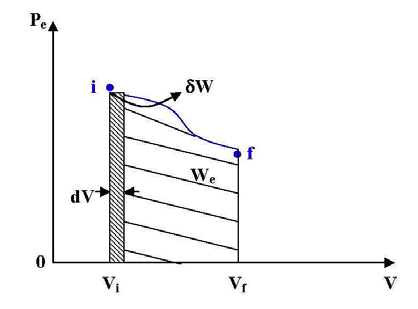
En la figura se ha representado la transformación efectuada por el sistema al expandirse de i a f, en el plano pv.
Se puede observar que el trabajo de expansión está representado gráficamente por el área delimitada por la transformación, las ordenadas extremas y el eje de las abscisas. De acuerdo a la convención de signos adoptada, se deduce que la expansión es positiva cuando se realiza contra el medio exterior, en cambio negativo (trabajo de compresión) cuando se realiza trabajo sobre el sistema y el incremento de volumen es negativo. Si la transformación realizada por el sistema al pasar de i a f es reversible, en todo su curso estará en equilibrio con el medio exterior, en consecuencia, la presión exterior estará igual a la del sistema Pe = P. La ecuación (2) se podrá escribir entonces:
![]() (3)
(3)
Donde P puede ser tanto la presión exterior como la del sistema. Cuando la transformación es irreversible, si hay expansión Pe < P, en cambio si hay compresión Pe > P. La ecuación (3) es en consecuencia, aplicable para el cálculo de expansión de un sistema termoelástico cerrado, cuando la transformación es reversible y abierta.
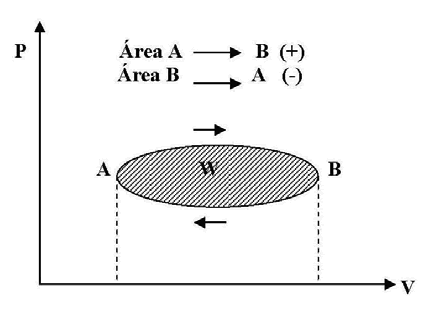
Cuando la transformación efectuada por el sistema es cerrada, o sea que el sistema ha recorrido un ciclo el trabajo total realizado será la suma algebraica de los trabajos correspondientes a las transformaciones parciales positivas y negativas. De esto se deduce que el trabajo total realizado durante el ciclo, está representado en un diagrama P-V por el área encerrada por el ciclo. Además se ve que si el ciclo se recorre en el sentido de las agujas del reloj, el trabajo es positivo, en cambio si se recorre en sentido contrario, el trabajo es negativo.
Dependencia del trabajo con respecto a la trayectoria
Si representamos en un diagrama P-V una transformación cualquiera por la cual el sistema pasa del estado inicial i al estado final f, podemos observar que existen varios caminos por los cuales el sistema puede pasar también de i a f.
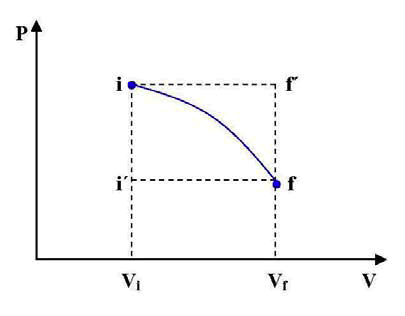
Por ej., la trayectoria i, i’, f y la trayectoria i, f´, f. En los tres casos, las áreas limitadas por las transformaciones serán diferentes, y en consecuencia los trabajos realizados por el sistema también lo serán. Esto significa que el trabajo realizado por un sistema no depende solamente de los estados inicial y final sino también de los estados intermedios, es decir, de la trayectoria. Para que la expresión 3 pueda ser integrada, es necesario conocer la dependencia de P con respecto a V, en la transformación que se considere. Se deduce también, que el trabajo no es una función real de las variables termodinámicas, es decir, no es una función de estado.
El trabajo elemental entonces, no es una diferencial exacta y por eso lo simbolizamos con las letras δW en lugar de dW para indicar que se trata de una diferencial inexacta. Como se dijo antes, el trabajo no puede estar contenido en un cuerpo, sino que aparece cuando éste sufre una transformación.