Ecuación de Mayer

Relaciones generales entre las capacidades caloríficas

Sabemos que el volumen es función de dos variables termodinámicas que pueden ser P y T es decir:

V = f(P,T)

Se cumplirá entonces que:

Reemplazando este valor de dV en la ecuación (3):

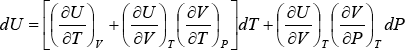(14)

Haciendo U = f(P,T)

(15)

Como los coeficientes de dT y dP en las ecuaciones (14) y (15) deben ser idénticos, se deduce que:

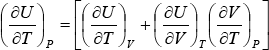
Despejando y reemplazando por su valor dado por (1)

(16)

De las ecuaciones (2) y (8) :

(17)

Restando la ecuación (16) de la (17), resulta:

(18)

Esta ecuación que relaciona las capacidades caloríficas a presión y volumen constante, es aplicable a cualquier sistema homogéneo de composición constante. Se puede simplificar cuando se conoce la ecuación de estado del sistema o sea la relación matemática entre P,V y T. El caso más sencillo es el de los gases ideales. Como dijimos que para un gas ideal se cumple la ecuación (4), aplicándola en la ecuación (18) se obtiene:

(19)

Para un mol de gas ideal, la ecuación de estado será:

P.V = R . T

Derivando con respecto a T a P constante:

Reemplazando en (19), resulta:

C_P – C_V = R (20)

Esta ecuación se denomina Ecuación de Mayer. Las capacidades caloríficas C_P y C_V son molares pues hemos considerado un mol de gas;

En los gases reales C_P - C_V no es exactamente igual a R, pero sus valores no se alejan tanto, salvo en condiciones donde las desviaciones del comportamiento ideal son muy grandes, por ejemplo a presiones elevadas y temperaturas bajas.