Transformaciones politrópicas

Procesos termodinámicos de gases ideales

En los gases ideales se pueden efectuar transformaciones en las cuales las cantidades de calor intercambiadas sean directamente proporcionales a las variaciones de temperaturas producidas. De acuerdo a la definición de calor específico, se cumplirá que:

δQ = m.c.dT (21)

donde la constante de proporcionalidad entre el calor y la temperatura es precisamente el calor especifico c que depende de la naturaleza del gas y de la transformación cumplida, pudiendo tomar valores entre -∞ y +∞ pasando por cero.
Si el calor específico permanece constante durante el proceso, la transformación recibe el nombre de “politrópica”.
Como ya dijimos que c puede tomar diferentes valores entre -∞ y +∞ en consecuencia, habrá tantas transformaciones politrópicas como valores pueda adoptar c.

Las principales transformaciones politrópicas que estudiaremos serán:

Isobárica o isobara. En la que: P= cte; dP= 0, c= c_P.

Isocórica o isocora. En la que: V= cte; dV=0, c= c_V.

Isotérmica o isoterma. En la que T= cte; dT= 0, c= ± ∞

Adiabática. En la que Q=0, c= 0

Ecuación general de las politrópicas

Si la masa del sistema se expresa en moles, la ecuación (21) se puede escribir:

δQ = n.c.dT (22)

en la cual c es ahora el calor especifico molar o capacidad específica molar y n el número de moles del sistema.

Para un mol de un gas ideal, si relacionamos las ecuaciones (7) y (22) podemos escribir:

δQ = C.dT = C_V.dT + PdV

haciendo pasaje de términos:

(C - C_V)dT = P.dV (23)

Esta ecuación representa la expresión del Primer Principio de la Termodinámica para una transformación politrópica cualquiera en la que interviene un gas ideal

En la ecuación C - Cv representa la diferencia de capacidades caloríficas molares de la politrópica y a volumen constante.

Para un mol de gas ideal, la ecuación de estado se escribe:

P.V = R.T

diferenciando: P.dV + V.0dP = R.dT (24)

multiplicando la ecuación (23) miembro a miembro por R, y reemplazando en ella el valor de R.dT dado por la (24):

(C - C_V)(P.dV + V.dP) = R.P.dV

Reemplazando R por su valor de la ecuación (20)

(C - C_V)(P.dV + V.dP) = (C_P - C_V).P.dV

De donde:

Luego

Si hacemos

(25) se cumple:

Integrando esta ecuación entre dos estados cualesquiera de la transformación que llamaremos 1 y 2

Efectuando la integración, y siendo n constante ya que así hemos supuesto las capacidades caloríficas molares:

Pasando a números:

o también:

P₂.V₂ⁿ = P₁.V₁ⁿ

generalizando para cualquier estado de la transformación se deberá cumplir que

P.Vⁿ = cte (constante) (26)

Esta expresión es la ecuación general de las politrópicas para gases ideales. El exponente n, definido por la ecuación (25) se denomina “exponente politrópico”.

La ecuación (26) relaciona las variables P y V, a continuación vincularemos las variables T y V.

Si en la ecuación (26) reemplazamos P por su valor obtenido de la ecuación de estado:

resulta:

luego se cumple que:

V.Tⁿ⁻¹ = cte (27)

Para relacionar P y T, reemplazamos en la ecuación (26) el valor de V obtenido de la ecuación de estado:

   ,    

de donde

P^1-n .Tⁿ = cte

aplicando raiz n:

(28)

Valores del exponente politrópico n para diferentes transformaciones

Transformaciones Isobáricas: C = C_P,

Transformaciones Isocóricas: C = C_V,

Transformaciones Isotérmicas: C= ∞,

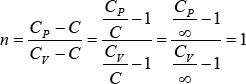
Transformaciones Adiabáticas: C = 0,

  (γ >1)

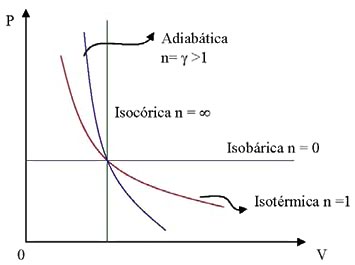
Vemos que los valores de n en las transformaciones politrópicas varían entre cero e infinito. Podemos representar gráficamente las distintas transformaciones en un diagrama P-V con sus correspondientes valores de n.