¿Qué es un cristal?
Antes del descubrimiento en 1982 de Shechtman del primer cuasicristal icosaédrico de orden de largo alcance, se pensaba que cristal era sinónimo de periodicidad. Los cristales, o sólidos ordenados, de hecho, se definen como arreglos periódicos de átomos, con la asignación de determinadas modificaciones a la periodicidad subyacente como en los casos de estructuras cristalinas moduladas inconmensurables y cristales compuestos inconmensurables. Casi dos décadas después, está bien establecido que la periodicidad no es necesaria para la producción de orden de largo alcance, pero todavía no está muy claro cómo exactamente se debe caracterizar la existencia de orden.
Señalando que los espectros de difracción de todos los cristales observados experimentalmente contiene picos de Bragg, la Unión Internacional de Cristalografía ha redefinido a un cristal como "... cualquier sólido que posea un diagrama de difracción esencialmente discreto." Los cristales que son periódicos en escala atómica se llaman explícitamente cristales periódicos, todos los demás se llaman cristales aperiódicos.
Esta definición no es simplemente otra empírica sino que también está motivada por la práctica común de tomar el conjunto de coeficientes de Fourier de densidad ρ (k) en vectores de onda k diferentes a cero como el parámetro de orden Landau, señalando una fase de transición de un estado líquido a un estado sólido ordenado. La nueva definición se hizo intencionalmente vaga por la inclusión de la palabra "esencialmente". Su propósito es sólo ser una definición de trabajo temporal hasta que una emerja una mejor comprensión de la cristalinidad. No tenemos que preocuparnos acerca de esta vaguedad porque sólo nos ocuparemos de cristales cuasiperiódicos, que son una subcategoría bien definida de estructuras, que satisfacen la nueva definición.
¿Qué es un cristal cuasiperiódico?
Los cristales cuyas funciones de densidad pueden ser ampliadas como superposición de un número numerable de ondas planas se llaman cristales casi periódicos. En particular, si tomando combinaciones lineales enteras de un número finito D de vectores de onda en esta expansión se puede abarcar todas lo demás, entonces el cristal es cuasiperiódico. Cada pico de difracción se indexa por enteros D. Los cristales periódicos son el caso especial donde la dimensión de indexación D es igual a la dimensión física real del cristal. Todos los cristales observados experimentalmente hasta la fecha son cuasiperiódicos.
Aunque aún no se ha acordado una nomenclatura oficial, una identifica claramente (al menos) dos categorías especiales entre la familia de cristales cuasiperiódicos: los cristales de estructuras moduladas inconmensurables y los cristales compuestos inconmensurables.
Los cristales de estructuras moduladas inconmensurables constan de (en promedio) una estructura básica ordenada que se perturba periódicamente -"modula"- donde el período de la modulación es inconmensurable con las periodicidades subyacentes de la estructura básica. Los diagramas de difracción de cristales inconmensurablemente modulados se caracterizan por tener un subconjunto de "reflexiones principales" - picos de Bragg que son significativamente más brillantes que el resto - que describen la estructura básica, y un conjunto de picos más débiles, llamados "satélites" derivados de la modulación. La estructura básica en sí misma puede ser periódica o no.
Los cristales compuestos inconmensurables, también llamados compuestos de intercrecimiento, se componen de dos o más subsistemas de interpenetración con periodicidades mutuamente inconmensurables. Cuando se los ve de forma independiente cada subsistema es un cristal en sí mismo, en particular en todos los ejemplos observados experimentalmente es un cristal periódico pero en teoría no necesariamente debe ser así, que es inconmensurablemente modulado debido a su interacción con los otros subsistemas. Los diagramas de difracción de cristales compuestos se caracterizan por la existencia de dos o más subconjuntos de reflexiones principales, causadas por las estructuras medias de los diferentes subsistemas, y un conjunto de reflexiones débiles causadas por las modulaciones.
¿Qué es un cuasicristal?
También hay cristales cuasiperiódicos (estrictamente aperiódicos) para los que una descripción en términos de una modulación de una estructura básica o de una composición de dos o más subestructuras bien sea inadecuada o imposible. Sosteniendo que uno debería referirse a todos los cristales como cuasicristales, independientemente de su grupo puntual de simetría. El modelo más común para este tipo de cristales es un mosaico quasiperiodico como el famoso mosaico de Penrose. Uno llena el espacio con "celdas unitarias" o "baldosas" de manera que se mantiene el orden de largo alcance sin periodicidad, y produce un diagrama de difracción esencialmente discreto.
Claramente, los cristales cuasiperiódicos que poseen simetrías que están prohibidas para los cristales periódicos, tales como los cristales icosaédricos, octogonales, decagonales y dodecagonales observados, no pueden ser formados por la modificación de una estructura periódica subyacente con la misma simetría, y por lo tanto son todos cuasicristales. Los cristales cuasiperiódicos sin simetrías prohibidas pueden formarse como una modificación de una estructura periódica, pero no necesariamente tienen por qué ser el caso.
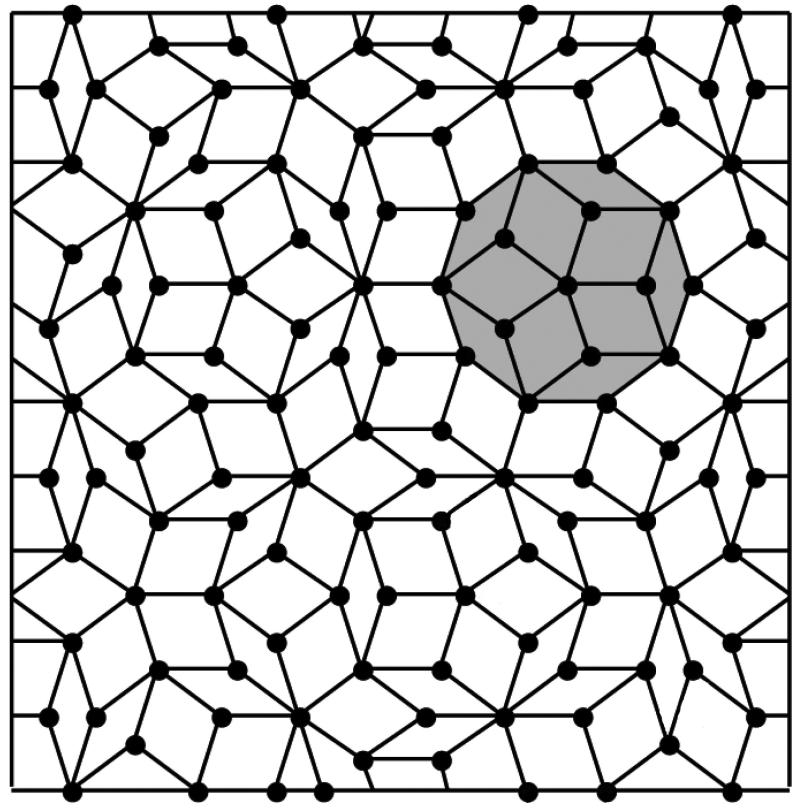
Cuasicristal bidimensional tipo Penrose creado utilizando sólo dos formas de mosaico: un rombo de grueso y un rombo delgado. La estructura propuesta por Roger Penrose carece de simetría de traslación y exhibe simetría rotacional de cinco veces no permitida en los cristales regulares. Imagen cortesía de la Universidad de Siracusa
Resulta que se observan experimentalmente cristales cuasiperiódicos con simetría cúbica, así como tetraedros, tetragonales y posiblemente también con simetría hexagonal, que no son cristales modulados ni cristales compuestos. Sus diagramas de difracción no muestran ningún subconjunto claro(s) de las reflexiones principales, sin embargo, no poseen ninguna simetría prohibida. Estos cristales no se forman mediante la modificación de una estructura periódica subyacente. Son tan intrínsecamente cuasiperiódicos como los cuasicristales que tienen simetrías prohibidas, y por lo tanto también deben ser considerados cuasicristales.
Desde un punto de vista teórico debería ser obvio que no hay nada de especial en grupos puntuales que están prohibidos para los cristales periódicos. Cualquier método que se utilice para generar una teselación cuasiperiódica con, por ejemplo, simetría 10 veces puede ser utilizado para generar mosaicos cuasiperiódicos con, por ejemplo, simetría 4 veces. De hecho, hay muchos ejemplos en la literatura de los modelos de mosaico de cuasicristales, con simetría de 2, 4, y de 6 veces, generados por todos los métodos estándar: reglas de acomodo, reglas de sustitución, el método de corte y proyección y por el método de la cuadrícula dual.
En conclusión, los cuasicristales en el espacio d-dimensional pueden tener cualquier subgrupo finito de O(d) como su grupo puntual. Es sólo la introducción de una periodicidad d-dimensiones lo que impone restricciones a las operaciones de simetría permitidas.