Una característica del orden cuasicristalino es la autosimilaridad de la estructura, que constituye un punto esencial en la mayoría de los modelos estructurales propuestos para estos materiales hasta la fecha. Esta autosimilaridad y, más específicamente, la escala en la que aparecen las características de autosimilaridad, se conoce como la simetría de inflación.
Esta autosimilitud se ilustra en la figura, que muestra un arreglo de quíntuple de puntos característicos del patrón de difracción de un cuasicristal icosaédrico y una construcción geométrica que tiene propiedades similares. (Bajo muchas condiciones de difracción, una simetría quíntuple como la que se muestra en la figura aparece de diez veces debido a la introducción de un centro de simetría de inversión.) En la figura b, los puntos de intersección de las líneas que unen los vértices del pentágono definen un nuevo pentágono. Su tamaño tiene una relación definida con la de la original, determinada por la relación τ -2, donde τ es la relación entre la diagonal y el lado del pentágono. Esta relación, que corresponde al número irracional (√5 + 1) / 2, ha sido conocida desde la antigüedad como la Proporción Aurea, y es implementada en artes como la pintura, la escultura y la arquitectura. El número áureo también describe las propiedades fundamentales de la secuencia de Fibonacci. Es notable que la construcción geométrica que se muestra en la Figura 2 b, conocida como una estrella de cinco puntas pitagórica, se expresa de forma natural por la disposición atómica espacial dentro de un cuasicristal, como se puede comprobar fácilmente por medio de una cuidadosa comparación con un patrón de difracción real, como el que se muestra en la Figura 2a. Otra característica notable de las estructuras cuasicristalinas es que pueden ser "simplificadas" levantándolas en un espacio dimensional superior (mayor que el espacio real físico en el que se manifiesta la cuasiperiodicidad).
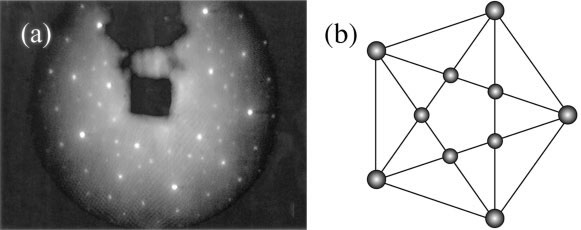
Figura 1. a) Patrón de difracción de electrones de baja energía de la superficie quíntuple de una fase icosaédrica de un cuasicristal Al - Pd -Mn, en el que la existencia de patrones pentagonales asociados con ejes quíntuple se puede ver claramente. b) Diagrama que ilustra la autosimilitud del patrón de difracción característico de un cuasicristal icosaédrico a lo largo de la zona de eje quíntuple.
Las agrupaciones que contienen varias decenas de átomos también se mencionan con frecuencia en la discusión de la estructura cuasicristalográfica. En particular, los clusters tipo Mackay y Bergman han sido identificados en una serie de aleaciones. Se ha propuesto que estos grupos poseen una estabilidad especial, que constituyen los pilares fundamentales de la construcción sólida, y que son en última instancia responsables de todas las propiedades físicas inusuales de los cuasicristales. Esta hipótesis se mantiene en estudio. La figura 2 a muestra la estructura de uno de tales cúmulos que pueden existir en el Al - Pd - Mn icosaédrico, y la figura 2 b muestra una disposición de estos grupos a lo largo del eje quíntuple. Hay que tener en cuenta que los grupos exhiben el mismo tipo de simetría de inflación como se ilustra en la Figura 1 b.
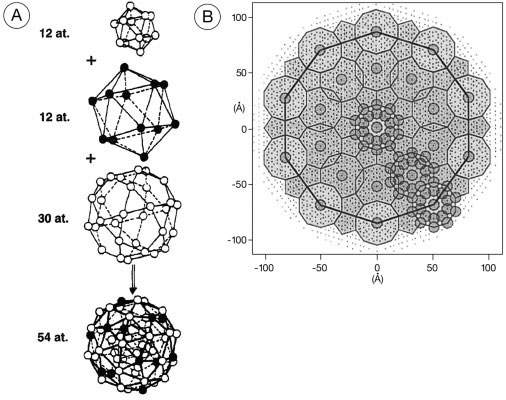
Figura 2. a) Estructura de un icosaedro Mackay. Grupos similares pueden ser identificados en la mayor parte de los Al - Pd - Mn y Al - Cu - Fe icosaédricos, aunque también pueden ser identificados otros tipos de grupos. b) Disposición de tipo Mackay icosaedrica que muestra la disposición jerárquica, autosimilar de la superposición de clusters.
El orden cuasiperiódico atómico no se limita sólo a la mayor parte del sólido, sino que está presente también en su superficie. Esto se manifiesta, por ejemplo, en los hábitos de crecimiento de monogranos, que en los sistemas icosaédricos a menudo muestran formas de dodecaedro o triacontaedro, como se predijo por la teoría. En sistemas decagonales, los hábitos de crecimiento suelen ser más anisotrópicos, y aún así pueden reflejar la naturaleza cuasicristalina.