Llegados a este punto se hace necesario enunciar dos leyes que como U d. verá se relacionan íntimamente con conceptos ya conocidos.
Primera ley de la termoquímica o Ley de Lavoisier-Laplace
“el calor necesario para descomponer una sustancia en sus elementos es igual, pero de sentido contrario, al que se necesita para volver a formarla”.
¿No es esto la ley de conservación de la energía?
Sí lo es, aplicado a un hecho concreto.
Y hablando de hechos concretos observemos el siguiente ejemplo:
H2 (g) + ½ O2 (g) → H2O (g) ∆H °f = -241,60 kJ/mol
De acuerdo a esta primera ley podemos escribir
H2O (g) → H2 (g) + ½ O2(g) ∆H °-1 = +241,60 kJ/mol
Como U d. vio la reacción en el sentido de la formación de agua cursa con un ∆H°f negativo mientras que en el sentido contrario lo hace con un ∆H ° positivo pero con igual valor absoluto (241,60 kJ/mol)
Segunda ley de la Termoquímica o Ley de Hess
En 1840 Hess postuló una ley absolutamente empírica: “el calor liberado a presión o volumen constante en una reacción química dada es una constante independientemente del número de etapas en que se realiza el proceso químico.”
Analice el texto y vuelva a pensar si no estamos nuevamente en presencia de otra aplicación de la ley de conservación de la energía que es la primera ley de la termodinámica.
Veamos un ejemplo:
Tratemos de hallar el ∆H de la siguiente reacción:
C (s) (grafito) + ½ O2(g) → CO (g) ∆H°r= ?
Esta es una reacción difícil de lograr en el laboratorio por lo que para hallar el
∆Hr aplicaremos la ley de Hess. Para ello acudamos a tablas en las que hallaremos
calculadas una cantidad muy importante de calores de reacción. Usaremos:
(1) C(s) (grafito) + O2 (g) → CO2 (g) ∆H°1 = -393,75 kJ/mol
(2) CO (g) + ½ O 2(g) → CO2(g) ∆H°2 = -282,98 kJ/mol
¿Qué podemos hacer con estas reacciones?
En primer lugar apliquemos la primera ley a la reacción (2) que quedará:
(-2) CO2 (g) → CO (g) + ½ O2(g) ∆H°-2= 282,98 kJ/mol
Luego de acuerdo a la ley de Hess podemos sumar la reacción (1) y la reacción (-2)
(1) C (s) (grafito) + O 2(g) → CO2 (g)
(-2) CO2 (g) → CO (g) + ½ O2 (g)
C (s) (grafito) + O2 (g) + CO2 (g) → CO2 (g) + CO (g) + ½ O2 (g)
Como se ve, hay especies en cantidades iguales a ambos lados como el CO2 (g) por lo que se pueden simplificar. Por otro lado hay 1 mol de O2 (g) a la izquierda y ½ mol de O2 (g) a la derecha por lo que balanceando queda ½ mol de O2 (g) a la izquierda.
La ecuación final será la que debíamos obtener:
C(s) (grafito) + ½ O2 (g) → CO (g)
¿Y el ∆H°r ?. Para su cálculo se procede de idéntica manera que la realizada arriba con las ecuaciones:
∆H°1 + ∆H°-2 = -393,75 kJ/m ol+282,98 kJ/mol = -463,01 kJ/mol
∆H°r = - 463,01 kJ/mol
Este mismo ejemplo se puede graficar por medio de un ciclo. Observe:
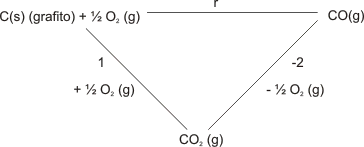
Gráfico número 21
A la letra r le corresponde un ∆H°r
Al número 1 le corresponde un ∆H°1
Al número -2 le corresponde un ∆H°-2
¿Qué otra operación sencilla podemos hacer con los calores de reacción?
Supongamos tener una reacción química teórica como la que sigue:
aA + bB → cC + dD ∆H°1
ahora observe la misma pero con éstas variaciones, que surgen de usar como factor común el número de moles de A (nA= a)
a/a A + b/a B → c/a C + d/a D DH °2= ???
En este caso el ∆H°2 = ∆H°1/a o lo que es lo mismo:
∆H°1 = a ∆H°2
Entalpías de combustión:
Son los calores generados cuando se queman hidrocarburos (que contienen C e H) en presencia de O2 (g) para dar CO2 (g) y H2O (l), y la combustión es completa.
Ejemplo :
C3H8 (g) + 5O2 (g) → 3CO2 (g) + 4H2O (l)
El calor que se produce es de 2217,90 kJ/mol y como se mide a 25ºC y 1 atm estando todas las sustancias en esas condiciones, ese valor es la entalpía estándar de combustión: ∆H°c= -2217,90 kJ/mol
Los calores de combustión estándar de los hidrocarburos se pueden hallar en tablas.
También podemos hallar valores de entalpías de combustión para sustancias como por ejemplo la glucosa que contiene carbono, oxígeno e hidrógeno.
C6H12O6 (s) + 6O2 (g) → 6CO2 (g) + 6H2O (l)
Las entalpías de formación son en general difícil de medir pero no las de combustión que se las mide en un calorímetro, aunque la restricción es que evidentemente deben manejarse sustancias que contengan carbono, hidrógeno y oxígeno.
Entalpías (energías) de enlace:
Hemos dicho que las energías de las uniones químicas representan una contribución muy importante a la energía interna de un sistema. Por ello si a las sustancias que componen el sistema (o a la sustancia) se le “rompen” varias (o todas) las uniones habrá un ∆E significativo y por ende un ∆H también significativo.
En ocasiones se desea obtener una estimación de la entalpía para una reacción en la que el valor de ∆H°f para un reactivo o producto no se conoce ni puede hallarse. ¿Cómo se soluciona el problema? Se acude a las energías de enlace. En éste método la energía de la molécula se atribuye esencialmente a la energía de los enlaces que ella posee y cuando reacciona lo hace debido a la ruptura o disolución de uno o más de estos enlaces. Luego el conocimiento relativo a la fuerza de los enlaces es útil para cuantificar los requerimientos energéticos de las reacciones. Pero en una reacción hay ruptura como hemos dicho y también (desde luego) formación de nuevos enlaces. ¿Cuál será el balance energético de estos procesos? Veamos un ejemplo sencillo como es la disociación de la molécula de H2 (g)
H2(g) → 2H (g) ∆H° = 434,72 kJ/mol
Esta será la energía de enlace de la molécula de H 2(g). Pero si intentamos formar nuevamente la molécula ¿cuánto calor (energía) necesitaremos?. Recuerde la primera ley de la termoquímica y dirá DH °= 434,72 kJ/mol. Por lo tanto generalizando cuando “formamos” uniones el sistema cede calor al entorno.
Podemos entonces hacer un balance entre las energías necesarias para “romper” uniones y las energías requeridas para “formar” uniones
Un ejemplo ayudará a entender mejor la pregunta:
CH4 (g) + 2 O2 (g) CO2 (g) + 2H2O (g) ∆H °= ???
Vamos a plantear la cuestión desde el punto de vista de los enlaces rotos y los formados. Luego efectuaremos el balance correspondiente:
Enlaces rotos |
Enlaces formados |
|---|---|
| 4 enlaces C–H c/u con 409,64 kJ/mol | 2 enlaces C=O c/u con –710,60 kJ/mol |
| 2 enlaces O=O c/u con 494,49 kJ/mol | 4 enlaces O–H c/u con –463,98 kJ/mol |
El cambio de entalpía total lo podemos calcular de la siguiente ∆H ° = 4 enlaces (C–H ) + 2 enlaces (O =O ) + 4 enlaces (O–H ) + 2 enlaces (O =O ) = -649,57 kJ/mol.
El valor experimentales –800,26 kJ/mol (lo que habla de que la anterior es un cálculo muy aproximado).