Termoquímica

Consideraciones previas

El estudio de la Termoquímica implica la introducción como concepto significativo, de la energía asociada a la estructuración química de la materia (¿arquitectura quizá se entiende mejor?). Este concepto se agrega así a los componentes térmicos de la energía (cinética, rotación, vibración) que eran los que considerábamos hasta ahora. Por lo tanto desde este momento debemos tener presente que la energía de un sistema (rigurosamente cualquiera como es obvio) tendrá una componente térmica y otra componente química o estructural:

E_T = componente térmica o energía térmica

E_Q= componente química o energía química

LUEGO:

ES= energía del sistema = E_T + E_Q

Ya dicho que la E_T es la que manejábamos hasta ahora pero la E_Q ¿estaba presente?:

Si, pero no intervenía por que no se consideraban procesos que incluyeran reacciones químicas

Sabemos que la energía de un sistema puede ser evaluada de acuerdo al tipo de proceso con que se trabaja como E o como H, pero aún así sigue siendo válido que siempre existirá una componente térmica y otra química.

De acuerdo a ello se puede plantear:

q_V = ∆E = ∆E_T + ∆E_Q

q_P = ∆H = ∆H _T + ∆H_Q

Energías térmicas y químicas: su interrelación con el sistema-entorno o medio ambiente.

La energía de un sistema tiene componentes químicos con su correspondiente Energía Química o estructural, Energías Térmicas en sus diferentes formas, y las Energías de los núcleos de los átomos (que por supuesto son las de mayor magnitud, pero como en los procesos que estudia la Termoquímica se mantienen constantes no las consideraremos). De acuerdo a ello vamos a esquematizar:

E_T = componente térmica o energías térmicas

E_Q = componente química o energía química

Luego:

E_S= ENERGÍA DEL SISTEMA = E_TÉRMICAS + E_QUÍMICAS

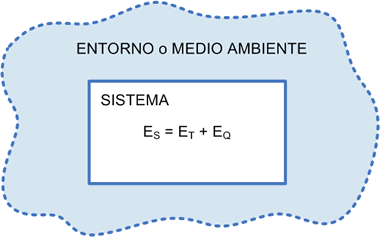
Gráfico número 13

Naturalmente cuando un sistema reacciona y cambia su composición química, habrá una variación en su energía química y podrá haberlo en las térmicas si la energía del proceso no se intercambia con el medio ambiente.

Los cambios de energías de un sistema pueden ser evaluados de acuerdo al tipo de proceso con que se trabaja tomando en cuenta E (energía interna, si es a volumen constante) o H (entalpía, a presión constante), pero aún así, sigue siendo válido que siempre existirá una componente térmica y otra química.

De acuerdo a ello se puede plantear:

q_V = ∆E = ∆E_T + ∆E_Q

q_P = ∆H = ∆H_T + ∆H_Q

Esto significa que en cualquier proceso, sea isobárico o isócoro, el calor intercambiado con el entorno puede provenir de la variación de energía de su componente térmico y/o del químico. Estrictamente si no hubiera variación en el componente químico no deberíamos hablar desde el punto de vista de la Termoquímica, aunque sí de la Termodinámica.

No obstante, y teniendo en cuenta lo expresado continuaremos el tratamiento considerando ambas opciones.

Variaciones en las energías térmicas

Tomaremos un sencillo ejemplo: 1 mol de H₂O (l) a 10ºC, presión constante y sin pérdida de m asa, se calienta a 50ºC.

En esas condiciones se necesita una cierta cantidad de calor que debe fluir del entorno, y consecuentem ente las Energías Térm icas del sistema que se plantea deben ir aumentando hasta que se llegue a la tem peratura indicada.

Pero aquí debe quedar claro que no hay variación en la energía química del sistema, ya que el componente se mantuvo inalterable [H₂O (l)], lo que significa decir que sus uniones intramoleculares no sufrieron variaciones.

Cabe aclarar que pueden inferirse variaciones en las energías intermoleculares, pero al no ser significativas frente a las intramoleculares, no las consideramos.

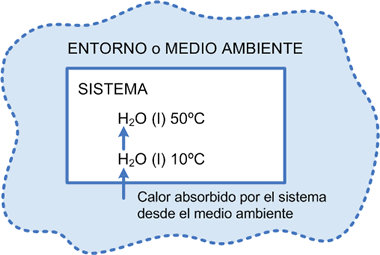
Gráfico número 14

Relaciones matemáticas sencillas entre las energías térmicas, la temperatura y la masa

¿Cómo podemos asociar matemáticamente la variación de la energía térmica con la temperatura y la masa? (tanto ∆E_T como ∆H_T).

Recuerde que habíamos definido:

y esto que es la capacidad calorífica molar, la podemos escribir también así:

∆H = C_P ∆T siendo válida para un mol de la sustancia en cuestión.

¿Cómo se expresa para una cantidad diferente de un mol?:

∆H = m c_P ∆T donde c_P es el calor específico (por gramo de sustancia).

Esto se puede deducir sencillamente así:

1 mol --------- C_P ∆T

n moles ------- x = n . C_P ∆T

pero:

ya que

¿Q ué ocurrirá si la transformación en lugar de ser isobárica (a P cte.) se realiza en forma isócora (a V cte.). ? U d. lo puede demostrar pero la relación matemática final será:

∆E = m c_V ∆T

Pero los ∆H y los de encontrados se refieren solo a cambios en la cantidad de calor aso ciado al sistema sin que hayan tomado parte para ello cambios estructurales o químicos, luego en forma rigurosa debemos escribir:

∆H T = m c_P ∆T

∆ET = m c_V ∆T