Comencemos tomando un ejemplo concreto: quememos gas natural (metano) a fin de utilizar la reacción en una máquina de combustión interna.
CH4 (g) + 2 O2 (g) → CO2 (g) + 2 H2O (l)
Esta es una reacción espontánea (tendremos que “iniciarla” como hacemos todas los días encendiendo la cocina en nuestras casas), y de ella podemos extraer para ser usada por la máquina una cierta cantidad de energía útil cuyo uso dependerá del grado de eficiencia de la misma (si se le entregan, por ejemplo 100 kJ, y se consigue la misma cantidad de trabajo su eficiencia sería del 100%)
Digamos desde ya que esto es imposible y la eficiencia es siempre mucho más pequeña.
Veamos ahora para otra reacción, y centrándonos en el trabajo útil como varía con la temperatura y cómo podemos manejar los datos que de ella se derivan.
Consideremos la reacción:
CaCO3 (s) → CaO (s) + CO2 (g)
Coloquemos el sistema a 1 atm. de presión y variemos la temperatura midiendo en cada caso el trabajo útil que resulte. Obtendremos una serie de datos los que se pueden graficar como sigue: (debe suponerse constancia de concentración de reactivos y productos en todos los puntos, consideración que todavía no podemos explicar).
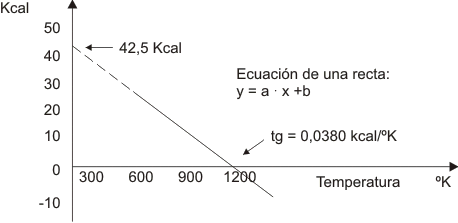
Gráfico número 25
Como usted ve se consigue una recta con ordenada al origen igual a +42,5 kcal y con una pendiente cuyo valor es -0,0380 kcal/K.
y = -0,0380 . T + 42,5
¿Qué significan cada uno de esos valores?
Si analizamos el ∆H de la reacción (suponiendo que la variación con la temperatura es despreciable) observamos que en nuestra ecuación de la recta la ordenada al origen será ∆H. Luego la misma va quedando:
y = -0,0380 T + ∆H
Al analizar el cambio de entropía que se genera entre productos y reactivos (para lo que podemos acudir a tablas) se ve que +0,0380 kcal/K es el cambio entrópico en esta reacción. Por lo tanto podemos escribir:
y = - ∆S . T + ∆H
y reordenando:
y = ∆H - T ∆S
Pero ¿qué será “y”?
Se dice que la capacidad de una reacción espontánea para dar trabajo útil, pude interpretarse desde el punto de vista de una pro piedad fundamental que se llama:
ENERGÍA LIBRE
y donde la cantidad de trabajo útil que puede obtenerse está limitada por la diferencia de la energía libre entre los productos y los reactivos.
El símbolo de la energía libre es: “G”
Y la variación de energía libre entre productos y reactivos será: ∆G Luego podemos escribir:
∆G = ∆H – T ∆S
Esta es la ecuación de Gibbs-Helmholtz
Obsérvese que estamos relacionando el contenido calórico del sistema (∆H) con la energía necesaria para “desordenar” el sistema (T∆S)
Gráfico número 26
La energía libre como todas las funciones termodinámicas es una función de estado y además es una propiedad extensiva (Usted mismo lo puede deducir).
Relación de la energía libre (G) con la temperatura y la presión
(no consideramos variaciones en la concentración):
Ya vimos como variaba la energía libre con la temperatura en el gráfico anterior. Allí habíamos predicho una presión constante e igual a 1 atm ya que si esta variaba el problema se hubiera complicado porque la energía libre depende en gran medida de la presión.
Volvam os a la reacción de descom posición de la piedra caliza (CaCO3 (s))
CaCO3 (s) CaO (s) + CO2 (g)
se ha visto que hay un cambio en la dirección en que avanza la reacción a medida que cambian la temperatura y la presión. Ampliemos esto conceptos.
A 25°C y 1 atm el ∆G es mayor que cero y la reacción no es espontánea, pero al aumentar la temperatura y disminuir la presión ∆G se hacer menor que cero y la reacción en esas condiciones es espontánea. Por lo tanto:
Conocer el ∆g de una reacción sirve para predecir la espontaneidad de la misma (o la direccionalidad)
Veamos la siguiente tabla: variaciones de ∆G con la temperatura y la presión para la reacción anterior:
T °C |
1 atm |
10-2 atm |
10-6 atm |
|---|---|---|---|
| 25° | +129,99 kJ | +120,33 kJ | +94,46 kJ |
| 200° | +102,41 kJ | +84,43 kJ | +48,07 kJ |
| 800° | +7,10 kJ | -34,69 kJ | -117,87 kJ |
| 1000° | -24,66 kJ | -74,4 kJ | -173,47 kJ |
Luego para la energía libre es necesario determinar la temperatura y la presión como ya hemos visto anteriormente para otras funciones termodinámicas, aunque cada una tiene su peculiaridad y esta última está fuertemente afectada por los cambios precisamente de temperatura y presión.
Los parámetros usados serán: 25°C y 1 atm de presión.
Accesoriamente debemos decir que también es importante definir la concentración de reactivos y productos como unitaria teniendo los sólidos por convención actividad uno.
Volvamos ahora sobre el concepto de espontaneidad y direccionalidad:
Dijimos que la reacción no era espontánea cuando el ∆G era mayor que cero refiriéndonos a la reacción tal cual está escrita, es decir en la dirección que se quiere lograr.
Al respecto veamos este ejemplo:
CaCO3 (s) CaO (s) + CO2 (g)
Con concentraciones de reactivos y productos unitarios y a 25ºC y 1 atm de presión, tiene ∆G = +129,99 kJ, luego La reacción en ese sentido no es espontánea, pero si lo es en el sentido contrario , por lo que en dichas condiciones se cumple (en forma espontánea)
CaO (s) + CO2 (g) CaCO3 (s) ∆G= -129,99 kJ
Cuando:
CaCO3 (s) CaO (s) + CO2 (g) a 800ºC y 10-6 atm
Tiene un ∆G = -117,87 kJ. la reacción es espontánea, o transcurre por si misma en esta dirección.
Ya nos vamos acercando a los criterios de espontaneidad tan necesarios en la química.
Manejo de los ∆G
Las leyes de la termoquímica pueden aplicarse a los cambios de energía libre.
Esto es sumamente importante a los efectos de los cálculos.
1.- ∆G es directamente proporcional a la cantidad de sustancia que se produce o reacciona. Recuerde que hemos dicho que la energía libre es una propiedad extensiva.
2.- En el ejemplo dado anteriormente de la descomposición del CaCO3 (s) podemos deducir que: el ∆G de una reacción es de la misma magnitud pero de signo contrario que el ∆G de la inversa.
3.- “Ley de H ess para el m anejo de la energía libre” (el encomillado se usó dado que el título no debe ser tomado textualmente, porque en la bibliografía no se lo define así; tómelo como una “versión libre” que cumple su objetivo: el manejo de los ∆G
Si puede considerarse una reacción como la suma de dos o m ás reacciones, el ∆G de la reacción global será la suma de los cambios de energía libre de las demás reacciones:
C (s) + ½ O2 (g) → CO (g) ∆G= -137,52 kJ
CO (g) + ½ O2 (g) → CO2 (g) ∆G= -257,07 kJ
C (s) + O2 (g) → CO2 (g) ∆G= -394,74 kJ
Como U d. ve se ha obtenido la formación del CO2 (g) a partir de sus elementos, lo que nos lleva a definir lo que ya conocemos para las entalpías.