La definición de la temperatura, el estado de agregación de los reactivos y productos y la presión deja todavía inconclusos la enumeración de otros aspectos que deben conocerse, ya que algunas sustancias como por ejemplo azufre puede existir en dos formas sólidas: rómbica y monoclínica.
Por lo tanto si pensamos que es necesario contar con datos de temperatura, presión, estado de agregación y características de ese estado de agregación es fácil imaginarse la dificultad para comparar entalpías.
Es más ¿cómo calcularlas si como sabemos el valor real de la energía interna nunca lo conocemos, luego tampoco podemos conocer el valor real de la entalpía?
Por ello se hizo necesario tener algún punto de referencia para los estados termodinámicos de los reactivos y productos. La elección de este punto de referencia es totalmente arbitraria y recibe el nombre de estado normal o estándar.
Por convenio internacional se establecieron las condiciones físicas baja las cuales se definen los estados normales o estándar, y ella s son:
Estado normal de un gas (puro): 1 atm y 25ºC
Estado normal de un líquido (puro): 1 atm y 25ºC
Estado normal de un sólido ( ** ): 1 atm y 25ºC
( ** ) puro y forma cristalina más estable.
Hemos definido los estados normales estándar pero ¿cómo podemos darle valores? (si ello es posible).
Sabiendo que la entalpía de una sustancia no se puede calcular (al menos sencillamente y mucho menos aún en los mejores cálculos con exactitud) el camino es establecer una convención arbitraria.
La misma para este caso se resume así (se insiste es arbitraria) la entalpía de una sustancia química elemental en su estado normal o estándar vale cero.
H° = 0
El exponente ° significa que los elementos se encuentran en él estado estándar
De acuerdo a lo expresado a 1 atm y 25ºC, el azufre rómbico (sólido), el cobre sólido, el bromo líquido, el O2 gaseoso, el H2 gaseoso y el Na sólido tienen entalpía igual a cero (0)
Pregunta con respuesta muy importante: ¿cuándo es válido esto?
a) Cuando se trabaja a temperatura constante (que se elige arbitrariamente, como por ej. 25º)
b) Si hay calentamiento o enfriamiento se debe elegir otra temperatura a la cual H °=0.
c) Sólo las entalpías de los elementos (no de los compuestos) en sus estados más estables es cero.
Ejemplo H (g) (hidrógeno monoatómico en estado gaseoso) no tiene entalpía igual a cero.
Hg (s) tampoco tiene entalpía igual a 0 (ya que su forma más estable es la líquida, piense sino en los termómetros clínicos).
En los dos ejemplos las sustancias se encuentran a 25ºC y 1 atm .
d) No se llevan a cabo transmutaciones nucleares ya que sino llegaríamos al absurdo de que una reacción como la que sigue no liberaría energía:
2 H2(g) He (g) donde ambas sustancias tienen de acuerdo con la convención indicada m ás arriba:
H° = 0
¡Pero esta reacción libera una cantidad muy importante de energía, y es la base del proceso que ocurre en el sol y se llama fusión nuclear.
Entalpía de las reacciones
La entalpía de una reacción es el cambio de entalpía que se produce durante la misma.
Cuando esta se lleva a cabo entre reactivos todos en sus estados estándar y se dan productos también en sus estados estándar la entalpía de la reacción es ∆H°

Gráfico número 18
Hemos graficado entalpías negativas pero U d. debe pensar también que existen las entalpías positivas, es decir calores de reacción positivos.
Entalpías de formación
Teniendo definida las entalpías estándar es fácil hablar de entalpías de formación. La definimos como “variación de entalpía que acompaña a una reacción de formación de una sustancia a partir de los elementos que la componen, estos en su estado más estable”.
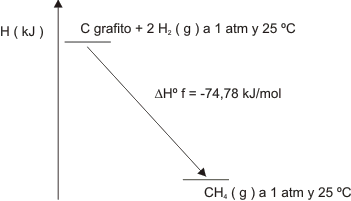
Gráfico número 19
Calculando numéricamente será:
H° CH4 (g) - (H° C (grafito) + H° H2 (g)) = -74,78 kJ/mol
Pero de lo visto anteriormente sabemos que H° del C(grafito) = 0 y que el H° del H2(g) es también igual a 0 luego:
H° del CH4 (g) - ( 0 + 0 ) = 74,89 kJ/mol
∆H°f CH 4(g) = - 74,89 kJ/mol
Este es un método efectivo para calcular entalpías usando los conceptos y convenciones estudiadas anteriormente.
Otro ejemplo:
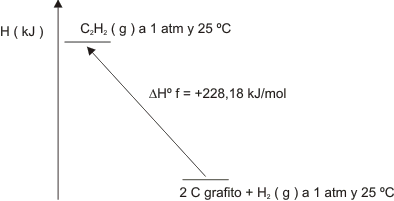
Gráfico número 20
¡Por fin una entalpía positiva!
Efectuemos el cálculo:
H° C2H2(g) - (H° C (grafito) + H° H2 (g)) = +226,51 kJ/mol
H° C2H2 (g) - ( 0 + 0 ) = +226,51 kJ/mol
∆H°f C2H2 (g) = +226,51 kJ/mol
A esta altura la pregunta podría ser: ¿las entalpías de formación calculadas de esta manera serán las entalpías reales de las sustancias?
Obviamente la respuesta es NO: recuerde que se han calculado por medio de una convención arbitraria (entalpías de las sustancias en su estado normal igual a 0), y esto ya de por sí da idea de que no son valores reales. Por otra parte, y de acuerdo a la convención, la entalpía del H 2(g) a 1 atm y 25ºC es cero y esto es contrario a nuestro criterio de que un mol de ese gas (o cualquier otro), tiene energías que podrán ser varias (traslación, rotación, vibración, London, etc.) lo cual hace que tenga una E (energía interna) real y por lo tanto una h (entalpía) también real luego la convención es absolutamente arbitraria y sobre ella se basan los cálculos.