Función de estado

Es aquella cuyo resultado no dependa del camino seguido sino del estado final y del inicial del sistema en estudio.

Para aclarar vamos a preguntarnos si la Energía Interna es una función de estado y evaluaremos dos sistemas sencillos:

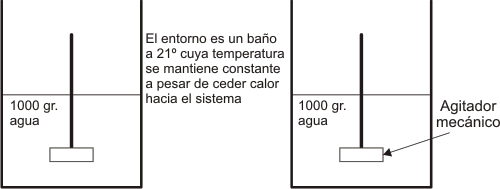
Gráfico número 10

T(i) = 20°C T(f) = 21°C

q = 999,43cal w =0

∆E = q + (-)w = 999,43 cal

T(i) = 20°C T(f) = 21°C

q=0 w = +4181,6 J = +999,43 cal

∆E = 0 + 999,43 cal = 999,43 cal

De aquí surgen dos hechos inmediatos:

a. se constata que E (energía interna) es una función de estado.

b. q (calor) en un caso tiene un valor finito y en el otro vale cero por que los caminos son distintos, y lo mismo ocurre con w (trabajo). Luego esto ayuda a entender (por más que un ejemplo sólo pueda parecer insuficiente) que el calor y el trabajo dependen necesariamente del camino que se sigue y por lo tanto no son función es de estado.

Pensemos ahora una situación intermedia donde primero llevamos el sistema de Ti= 20ºC a Tf= 20,5ºC poniéndolo en contacto con un baño que está a esa temperatura y luego se agita mecánicam ente para que la T pase de 20,5ºC a 21ºC.

Es evidente que los valores de “q” y “w” resultantes serán distintos de los planteados arriba pero el valor de ∆E seguirá siendo igual a 999,43 cal.

Finalmente: los pasos podrán ser cualesquiera pero el resultado será el mismo y “q” y “w” no son función de estado, dependiendo siempre del camino que se recorre.

Los ejemplos sobre los cuales hemos explicado los conceptos de calor, trabajo y energía interna ofrecen otra característica que se pude considerar: ¿en cuánto tiempo se realizan? Hay una respuesta inmediata: todos los procesos reales ocurren en un tiempo finito (medible perfectamente). A demás, esos procesos se realizan en forma irreversible. ¿Por qué? : piense simplemente en qué mecanismo se le ocurriría para “ceder” el calor ganado por el sistema y perdido por el entorno de modo que éste lo recuperara sin ninguna pérdida. Si Ud. lo encuentra eso sería un proceso reversible.

En termodinámica un proceso reversible es el análogo de un movimiento sin frotación en mecánica, luego ambos son ideales:

Un proceso termodinámicamente reversible es aquel que se realiza en forma infinitamente lenta, de modo que el sistema se encuentre siempre en equilibrio con el entorno o medio ambiente.

Diferentes formas de trabajo

A pesar de que sólo usaremos para calcular el trabajo la expresión w = P. ∆V (o la que se encuentra arriba en esta misma página), que se refieren al trabajo de expansión, no es esta la única expresión posible. Si tomáramos para estudiar otros sistemas (no sólo gases ideales) con otras sustancias en cualquier estado de la materia, podríamos hallar otros trabajos. En general esos “otros” trabajos se los llama (como ya sabemos) trabajo útil o (término nuevo) aprovechable.

La siguiente es la m ás usada de las expresiones para este tipo de trabajo:

w_útil = cualquier trabajo que no sea de expansión de un gas contra la Presión atmosférica.

¿Pero, cual será la expresión general de las variaciones de la Energía Interna si existieran trabajos de expansión “no útil” y trabajos útiles?

∆E = q + w_exp + w_útil

En verdad esta última ecuación, nunca la usaremos en forma completa, ya que en este texto no nos plantearemos sistemas tan complejos.

¿Cuántos tipos de trabajo distintos del de expansión podemos nombrar? :

Trabajo

• Eléctrico
• Osmótico
• Luz
• Químico
• Muscular
• Gravitatorio
• De superficie

No efectuaremos comentarios sobre ellos ni plantearemos el cálculo de cada uno de, ya que la lista anterior se da al sólo efecto enunciativo y para que se conozca la existencia de otros trabajos que no son los de expansión.

El calor en las transformaciones isobáricas

Una transformación isobárica es aquella que se verifica a P = cte. Podemos escribir entonces si sólo hay trabajo de expansión (o compresión):

∆E = q_p + w = q + (–p ∆V) = q_p + [–p (V_f – V_i)]

Analicemos término por término:

E es independiente del camino

p es independiente del camino

V_f es independiente del camino

V_i es independiente del camino

Luego ∆V será también independiente del camino

Debemos concluir que q_p en este caso será también función de estado (cuidado no generalice ya que es un ejemplo particular) Hemos hallado entonces un calor que es función de estado y esto ocurre porque se definió el camino (P = cte.)

Para gases P . ∆V = P.V_B - P.V_A

Pero como: P.V_B = n_B.R.T y que P.V_A = n_A.R.T podemos reemplazar y queda:

P *(V_B – V_A) = (n_B- n_A) R.T = ∆n R.T

por lo tanto DE = q_p + ∆n R.T donde P y T son constantes.