Daremos a continuación la expresión matemática de la Primera ley o Primer principio. En realidad, como se verá, calcularemos la variación de la energía interna (∆E) de un sistema.
Como se ha dicho anteriormente, al ocurrir un cambio de energías (calor y trabajo, o una sola de ellas) la variación de energía del sistema (que es el que interesa) y el que en definitiva es la variación de ∆E que se busca conocer, será ∆Es = ∑EI.
Esta sumatoria de energías intercambiadas, es como su nombre lo indica ∑EI = calor + trabajo. Esto es, la energía en forma de calor que se ganó o perdió más la energía en forma de trabajo que se ganó o perdió.
Veamos estos ejemplos:
Caso 1:
Un sistema “recibe” calor por lo tanto según la convención es positivo y realiza Trabajo (expansión), por el sistema hacia el entorno, luego es negativo.
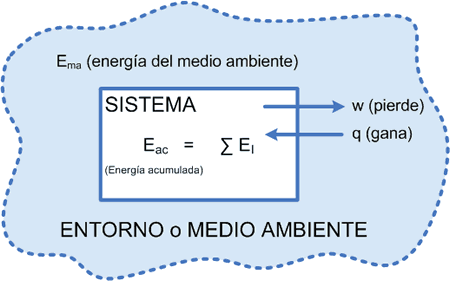
Gráfico número 6
¿Qué ocurrió en el Sistema luego de haberse completado el intercambio de Energía?
Recibió calor: aumentó su energía interna realizó un trabajo (por el sistema): perdió energía interna.
Luego para conocer en cuánto varió la energía interna (∆E) del sistema debemos calcular la sumatoria de energías intercambiadas, pero para ello debe recordarse la convención de signos, donde el Calor es positivo y el Trabajo (de expansión) que según el cálculo es positivo, debe cambiarse su signo a negativo; luego la sumatoria será:
∑EI = ∆Es = ∆E = q + w
En esta ecuación se advierte que q debe mantenerse con el signo según el proceso (aumentó) y w que según el cálculo será positivo debe “cambiarse su signo” según la convención adoptada.
Caso 2:
Un sistema “cede” cierta cantidad de Calor (por lo tanto es “negativo”) y el entorno realiza “sobre el sistema” un cierto Trabajo (por lo tanto el sistema recibe energía y ese trabajo debe ser positivo).
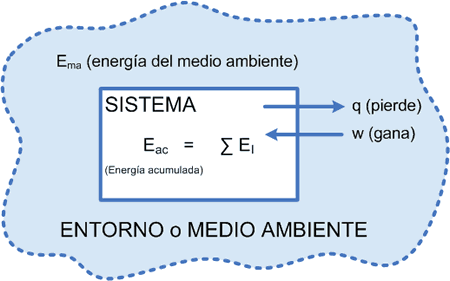
Gráfico número 7
En el balance hallaremos: (“q” es negativo y “w” es positivo).
Cedió calor (exotérmico), luego disminuyó su energía interna recibió un trabajo (sobre el sistema): aumentó su energía interna
Por lo tanto:
∑EI = ∆E = q + w
donde “q” debe mantenerse con el signo de acuerdo al proceso y “w” debe sumarse ya que aumenta la E.
Caso 3:
Un sistema “cede” cierta cantidad de calor (proceso exotérmico) y realiza un trabajo (luego pierde energía).
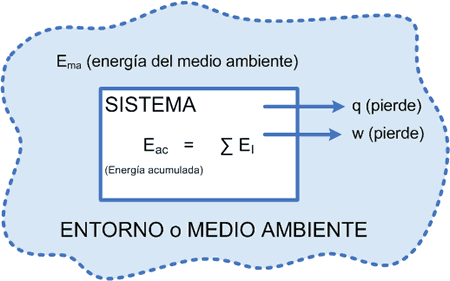
Gráfico número 8
En el balance será:
Cedió calor (exotérmico), luego perdió energía interna realizó un trabajo (por el sistema) luego perdió energía interna
Por lo tanto:
∑EI = ∆E = q + w
Caso 4:
Un sistema “recibe” calor (proceso endotérmico) aumentando su energía y el medio ambiente realiza “sobre” él un trabajo, lo cual también aumenta la energía.
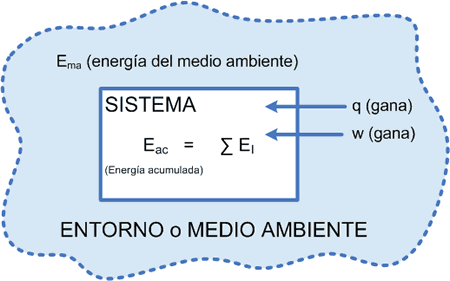
Gráfico número 9
En el balance, quedará:
Recibió calor (proceso endotérmico) aumentando su energía recibió un trabajo (sobre el sistema) aumentando su energía
Por lo tanto:
∑EI = ∆E = q + w
Expresión de la primera ley considerando los trabajos posibles
∆E = ∑EI = ∆Es= q + wexp + wútil
Donde wútil es cualquier trabajo que no sea de expansión contra la presión atmosférica (no tome en cuenta el ejemplo particular anterior ya que sólo se lo hizo con fines didácticos).
Un ejemplo de un sistema muy sencillo (y por lo mismo muy común) es el referido a un mol de gas ideal: en este, sabemos que la única energía existente es la cinética de cada un a de las moléculas y que para un mol de gas será igual a:
Ec= 3/2 R T
y que para una molécula será:
Ec = 3/2 k T
donde k= constante de Boltzman y también se puede demostrar que R(constante de los gases)= NA.k donde NA= número de Avogadro.
Luego la Energía interna de un gas ideal es fácilmente calculable por medio de estas fórmulas ya descriptas, pero el problema se complica cuando en lugar de este modelo acudimos por ejemplo a un gas real. Allí nuestro postulado de asignar sólo energía cinética no es suficiente ya que existen otras muchas formas de energía, y todas de acuerdo al enunciado forman parte de la energía interna, luego es lógico pensar en la dificultad de calcularlas una a una y sumarlas.
Afortunadamente la Termodinámica clásica no le interesa el valor real porque sólo se ocupa de cuantificar los cambios energéticos, como habrá quedado claro en los ejemplos dados anteriormente.